Matura z matematyki 2017 – Maj podstawowy
Liczba 58⋅16−2 jest równa
Liczba \(\sqrt[3]{54}-\sqrt[3]{2}\) jest równa
Liczba \(2{{\log }_{2}}3-2{{\log }_{2}}5\) jest równa
Liczba osobników pewnego zagrożonego wyginięciem gatunku zwierząt wzrosła w stosunku do liczby tych zwierząt z 31 grudnia 2011 r. o 120% i obecnie jest równa 8910. Ile zwierząt liczyła populacja tego gatunku w ostatnim dniu 2011 roku?
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Równość \({{\left( x\sqrt{2}-2 \right)}^{2}}={{\left( 2+\sqrt{2} \right)}^{2}}\) jest
Do zbioru rozwiązań nierówności (x4+1)(2−x)>0 nie należy liczba
Wskaż rysunek, na którym jest przedstawiony zbiór wszystkich rozwiązań nierówności 2−3x≥4 .
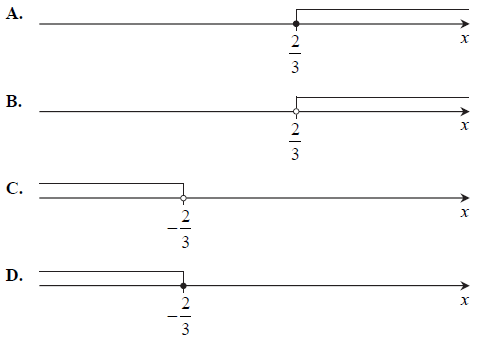 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Równanie x(x2−4)(x2+4)=0 z niewiadomą x
Miejscem zerowym funkcji liniowej \(f\left( x \right)=\sqrt{3}\left( x+1 \right)-12\) jest liczba
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej f(x)=ax2+bx+c , której miejsca zerowe to: −3 i 1.
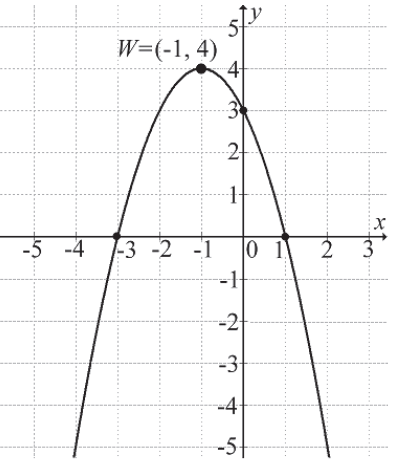
Współczynnik c we wzorze funkcji f jest równy:
Na rysunku przedstawiono fragment wykresu funkcji wykładniczej f określonej wzorem f(x)=ax. Punkt A=(1,2) należy do tego wykresu funkcji.
Podstawa a potęgi jest równa
W ciągu arytmetycznym (an ) , określonym dla n≥1, dane są: a1=5 , a2=11. Wtedy
Dany jest trzywyrazowy ciąg geometryczny (24,6,a−1). Stąd wynika, że
Jeśli m = sin50° , to
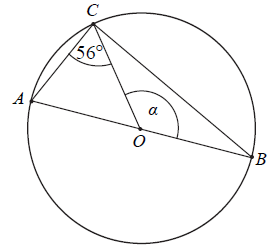
Na okręgu o środku w punkcie O leży punkt C (zobacz rysunek). Odcinek AB jest średnicą tego okręgu. Zaznaczony na rysunku kąt środkowy α ma miarę
W trójkącie ABC punkt D leży na boku BC, a punkt E leży na boku AB. Odcinek DE jest równoległy do boku AC, a ponadto |BD|=10 , |BC|=12 i |AC|=24 (zobacz rysunek).
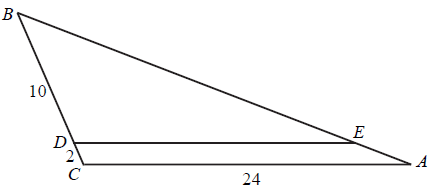
Długość odcinka DE jest równa
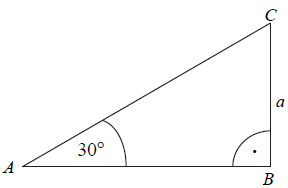
Obwód trójkąta ABC, przedstawionego na rysunku, jest równy
Na rysunku przedstawiona jest prosta k, przechodząca przez punkt A=(2,−3) i przez początek układu współrzędnych, oraz zaznaczony jest kąt α nachylenia tej prostej do osi Ox.
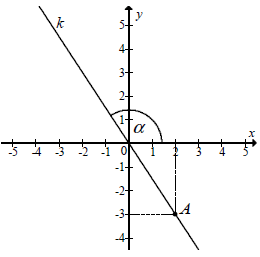
Zatem
Na płaszczyźnie z układem współrzędnych proste k i l przecinają się pod kątem prostym w punkcie A=(−2,4) . Prosta k jest określona równaniem \(y=-\frac{1}{4}x+\frac{7}{2}\). Zatem prostą l opisuje równanie
Dany jest okrąg o środku S=(2,3) i promieniu r=5 . Który z podanych punktów leży na tym okręgu?
Pole powierzchni całkowitej graniastosłupa prawidłowego czworokątnego, w którym wysokość jest 3 razy dłuższa od krawędzi podstawy, jest równe 140. Zatem krawędź podstawy tego graniastosłupa jest równa
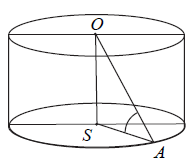
Promień AS podstawy walca jest równy wysokości OS tego walca. Sinus kąta OAS (zobacz rysunek) jest równy
Dany jest stożek o wysokości 4 i średnicy podstawy 12. Objętość tego stożka jest równa
Średnia arytmetyczna ośmiu liczb: 3, 5, 7, 9, x, 15, 17, 19 jest równa 11. Wtedy
Ze zbioru dwudziestu czterech kolejnych liczb naturalnych od 1 do 24 losujemy jedną liczbę. Niech A oznacza zdarzenie, że wylosowana liczba będzie dzielnikiem liczby 24. Wtedy prawdopodobieństwo zdarzenia A jest równe
Wykaż, że liczba 42017 + 42018 + 42019 + 42020 jest podzielna przez 17.
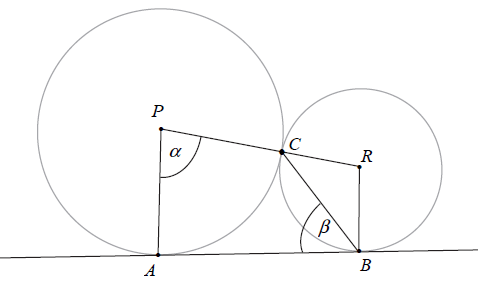
Treść dostępna po opłaceniu abonamentu.Dane są dwa okręgi o środkach w punktach P i R , styczne zewnętrznie w punkcie C. Prosta AB jest styczna do obu okręgów odpowiednio w punktach A i B oraz |∢APC|=α i |∢ABC|=β (zobacz rysunek). Wykaż, że α=180°−2β .
 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Funkcja kwadratowa f jest określona dla wszystkich liczb rzeczywistych x wzorem f(x)=ax2+bx+c . Największa wartość funkcji f jest równa 6 oraz \(f\left( -6 \right)=f\left( 0 \right)=\frac{3}{2}\) . Oblicz wartość współczynnika a.
Treść dostępna po opłaceniu abonamentu.Przeciwprostokątna trójkąta prostokątnego ma długość 26 cm, a jedna z przyprostokątnych jest o 14 cm dłuższa od drugiej. Oblicz obwód tego trójkąta.
Treść dostępna po opłaceniu abonamentu.W ciągu arytmetycznym (an), określonym dla n≥1, dane są: wyraz a1= 8 i suma trzech początkowych wyrazów tego ciągu S3= 33 . Oblicz różnicę a16−a13 .
Treść dostępna po opłaceniu abonamentu.Dane są punkty A = (−4,0) i M = (2,9) oraz prosta k o równaniu y = −2x +10 . Wierzchołek B trójkąta ABC to punkt przecięcia prostej k z osią Ox układu współrzędnych, a wierzchołek C jest punktem przecięcia prostej k z prostą AM. Oblicz pole trójkąta ABC.
Treść dostępna po opłaceniu abonamentu.Ze zbioru wszystkich liczb naturalnych dwucyfrowych losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia, że wylosujemy liczbę, która jest równocześnie mniejsza od 40 i podzielna przez 3. Wynik zapisz w postaci ułamka zwykłego nieskracalnego.
Treść dostępna po opłaceniu abonamentu.W ostrosłupie prawidłowym trójkątnym wysokość ściany bocznej prostopadła do krawędzi podstawy ostrosłupa jest równa \(\frac{5\sqrt{3}}{4}\) , a pole powierzchni bocznej tego ostrosłupa jest równe \(\frac{15\sqrt{3}}{4}\) . Oblicz objętość tego ostrosłupa.
Treść dostępna po opłaceniu abonamentu.- Matura z matematyki 2017 – Maj podstawowa
- Matura z matematyki 2016 – Maj podstawowa
- Matura z matematyki 2015 – Maj podstawowa
- Matura z matematyki 2014 – Maj podstawowa
- Matura z matematyki 2013 – Maj podstawowa
- Matura z matematyki 2012 – Maj podstawowa
- Matura z matematyki 2011 – Maj podstawowa
- Matura z matematyki 2010 – Maj podstawowa
- Matura z matematyki 2009 – Maj podstawowa
- Matura z matematyki 2008 – Maj podstawowa
- Matura z matematyki 2007 – Maj podstawowa
- Matura z matematyki 2006 – Maj podstawowa
- Matura z matematyki 2005 – Maj podstawowa
- Matura z matematyki 2003 – Maj podstawowa




