Matura z matematyki 2012 – Sierpień podstawowa
Zobacz arkusz i odpowiedzi z sierpniowej matury z matematyki 2012 już teraz online. Matury z poprzednich lat są idealnym materiałem ćwiczeniowym do kolejnych egzaminów maturalnych.
Arkusz i odpowiedzi Centralnej Komisji Edukacyjnej
- Matura z matematyki sierpień 2012 – Poziom Podstawowy – Arkusz CKE
- Matura z matematyki sierpień 2012 – Poziom Podstawowy – Odpowiedzi CKE
Warto wiedzieć!
- Niektóre działy z matematyki co roku pojawiają się na maturze – masz więcej czasu na nauczenie tych konkretnych zagadnień matematycznych.
- Zwróć uwagę na zadania, które pojawiają się co roku. Zauważ, że zmieniają się tylko dane do zadań.
Matura z matematyki sierpień 2012 – Zadania i odpowiedzi
Długość boku kwadratu k2 jest o 10% większa od długości boku kwadratu k1. Wówczas pole kwadratu k2 jest większe od pola kwadratu k1
Iloczyn \({9^{ – 5}} \cdot {3^8} \) jest równy
Liczba \({\log _3}27 – {\log _3}1\) jest równa
Liczba \({\left( {2 – 3\sqrt 2 } \right)^{\;2}}\) jest równa
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Liczba (-2) jest miejscem zerowym funkcji liniowej \(f\left( x \right) = mx + 2\) Wtedy
Wskaż rysunek, na którym jest przedstawiony zbiór rozwiązań nierówności \(\left| {x + 4} \right| \le 7\)
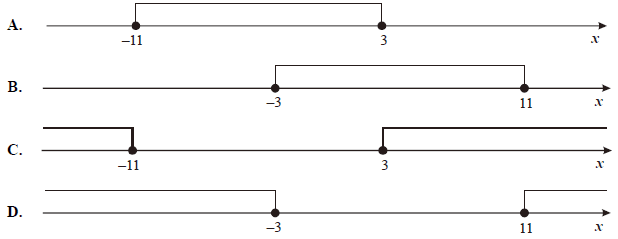 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Dana jest parabola o równaniu \(y = {x^2} + 8x – 14\). Pierwsza współrzędna wierzchołka tej paraboli jest równa
Wskaż fragment wykresu funkcji kwadratowej, której zbiorem wartości jest \(\left\langle { – 2,} \right.\left. { + \infty } \right)\)
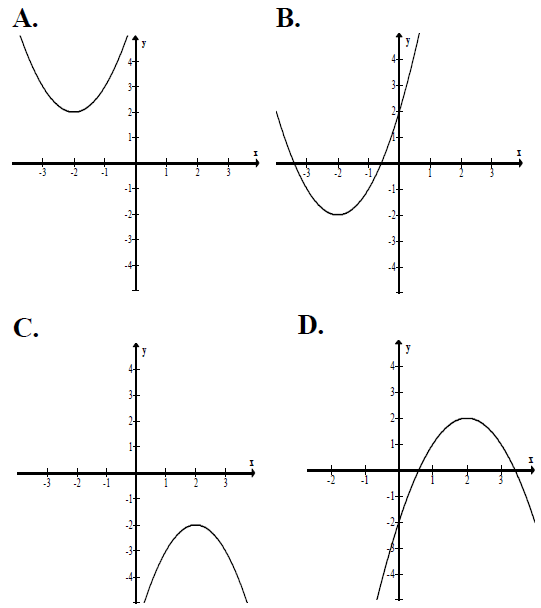 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Zbiorem rozwiązań nierówności \(x\left( {x + 6} \right) < 0\) jest
Wielomian \(W\left( x \right) = {x^6} + {x^3} – 2\) jest równy iloczynowi
Równanie \(\frac{{\left( {x + 3} \right) \cdot \left( {x – 2} \right)}}{{\left( {x – 3} \right) \cdot \left( {x + 2} \right)}} = 0\) ma
Dany jest ciąg \(\left( {{a_n}} \right)\) określony wzorem \({{a}_{n}}=\frac{n}{{{\left( -2 \right)}^{\,n}}}\) dla n≥1. Wówczas
W ciągu geometrycznym (an) dane są: a1=36 , a2=18 . Wtedy
Kąt \(\alpha\) jest ostry i \(\sin \alpha = \frac{7}{{13}}\). Wtedy \(tg\alpha \) jest równy
W trójkącie prostokątnym dane są długości boków (zobacz rysunek). Wtedy
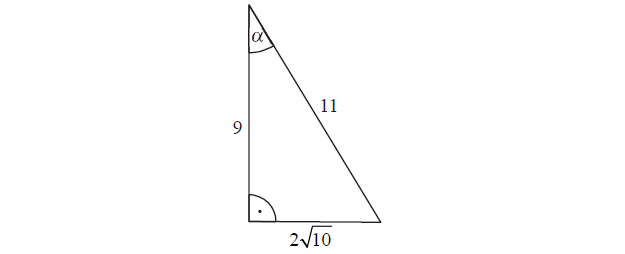
Przekątna AC prostokąta ABCD ma długość 14. Bok AB tego prostokąta ma długość 6. Długość boku BC jest równa
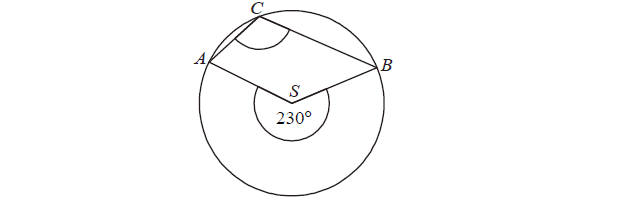
Punkty A , B i C leżą na okręgu o środku S (zobacz rysunek). Miara zaznaczonego kąta wpisanego ACB jest równa
Długość boku trójkąta równobocznego jest równa \(24\sqrt 3 \) . Promień okręgu wpisanego w ten trójkąt jest równy
Wskaż równanie prostej przechodzącej przez początek układu współrzędnych i prostopadłej do prostej o równaniu \(y = – \frac{1}{3}x + 2\)
Punkty B = (-2, 4) i C = (5, 1) są dwoma sąsiednimi wierzchołkami kwadratu ABCD. Pole tego kwadratu jest równe
Dany jest okrąg o równaniu \({\left( {x + 4} \right)^2} + {\left( {y – 6} \right)^2} = 100\). Środek tego okręgu ma współrzędne
Objętość sześcianu jest równa 64. Pole powierzchni całkowitej tego sześcianu jest równe
Przekrój osiowy stożka jest trójkątem równobocznym o boku a. Objętość tego stożka wyraża się wzorem
Pewna firma zatrudnia 6 osób. Dyrektor zarabia 8000 zł, a pensje pozostałych pracowników są równe: 2000 zł, 2800 zł, 3400 zł, 3600 zł, 4200 zł. Mediana zarobków tych 6 osób jest równa
Ze zbioru {1, 2, 3, 4, 5, 6, 7, 8, 9,10,11,12,13,14,15} wybieramy losowo jedną liczbę. Niech p oznacza prawdopodobieństwo otrzymania liczby podzielnej przez 4. Wówczas
Rozwiąż nierówność \({x^2} – 8x + 7 \ge 0\)
Treść dostępna po opłaceniu abonamentu.Rozwiąż równanie \({x^3} – 6{x^2} – 9x + 54 = 0\)
Treść dostępna po opłaceniu abonamentu.Pierwszy wyraz ciągu arytmetycznego jest równy 3, czwarty wyraz tego ciągu jest równy 15. Oblicz sumę sześciu początkowych wyrazów tego ciągu.
Treść dostępna po opłaceniu abonamentu.W trójkącie równoramiennym ABC dane są \(\left| AC \right|=\left| BC \right|=6\quad i\quad \left| \sphericalangle ACB \right|=30{}^\circ \) (zobacz rysunek). Oblicz wysokość AD trójkąta opuszczoną z wierzchołka A na bok BC.
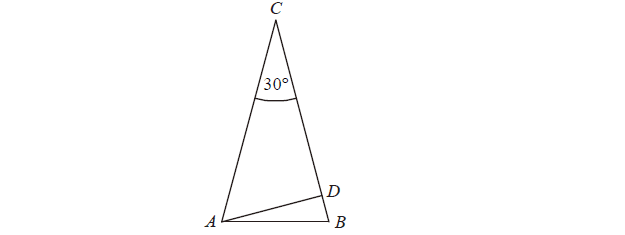 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
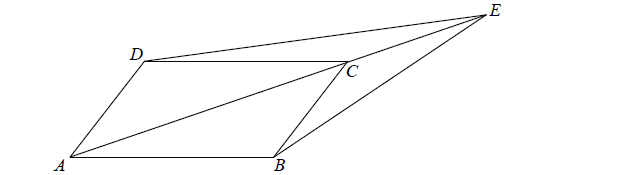
Dany jest równoległobok ABCD. Na przedłużeniu przekątnej AC wybrano punkt E tak, że \(\left| {CE} \right| = \frac{1}{2}\left| {AC} \right|\) (zobacz rysunek). Uzasadnij, że pole równoległoboku ABCD jest cztery razy większe od pola trójkąta DCE.
 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Wykaż, że jeżeli c < 0 , to trójmian kwadratowy \(y = {x^2} + bx + c\) ma dwa różne miejsca zerowe.
Treść dostępna po opłaceniu abonamentu.Dany jest trójkąt równoramienny ABC, w którym |AC| = |BC| oraz A = (2,1) i C = (1,9). Podstawa AB tego trójkąta jest zawarta w prostej y=0,5x. Oblicz współrzędne wierzchołka B.
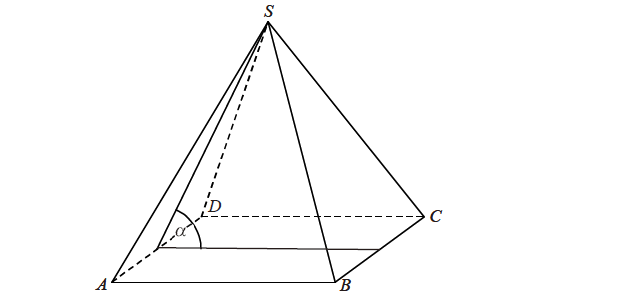
Treść dostępna po opłaceniu abonamentu.W ostrosłupie prawidłowym czworokątnym ABCDS o podstawie ABCD i wierzchołku S trójkąt ACS jest równoboczny i ma bok długości 8. Oblicz sinus kąta nachylenia ściany bocznej do płaszczyzny podstawy tego ostrosłupa (zobacz rysunek).
 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Kolarz pokonał trasę 114 km. Gdyby jechał ze średnią prędkością mniejszą o 9,5 km/h, to pokonałby tę trasę w czasie o 2 godziny dłuższym. Oblicz, z jaką średnią prędkością jechał ten kolarz.
Treść dostępna po opłaceniu abonamentu.- Matura z matematyki 2017 – Maj podstawowa
- Matura z matematyki 2016 – Maj podstawowa
- Matura z matematyki 2015 – Maj podstawowa
- Matura z matematyki 2014 – Maj podstawowa
- Matura z matematyki 2013 – Maj podstawowa
- Matura z matematyki 2012 – Maj podstawowa
- Matura z matematyki 2011 – Maj podstawowa
- Matura z matematyki 2010 – Maj podstawowa
- Matura z matematyki 2009 – Maj podstawowa
- Matura z matematyki 2008 – Maj podstawowa
- Matura z matematyki 2007 – Maj podstawowa
- Matura z matematyki 2006 – Maj podstawowa
- Matura z matematyki 2005 – Maj podstawowa
- Matura z matematyki 2003 – Maj podstawowa




