Matura z matematyki 2011 – Maj podstawowy
Czy zgodzisz się, że matura z matematyki 2011 nie była trudna? Zobacz zadania maturalne i odpowiedzi już teraz online!
Arkusz i odpowiedzi Centralnej Komisji Edukacyjnej
- Matura z matematyki 2011 – Maj Poziom Podstawowy – Arkusz CKE
- Matura z matematyki 2011 – Maj Poziom Podstawowy – Odpowiedzi CKE
Czas na analizę zadań maturalnych. Jakie zadania były proste, a które przysporzyły najwięcej problemów dla maturzystów? Zobacz i oceń.
Matura z matematyki 2011 – Zadania i odpowiedzi online
Wskaż nierówność, którą spełnia liczba \(\pi\)
Pierwsza rata, która stanowi 9% ceny roweru, jest równa 189 zł. Rower kosztuje
Wyrażenie \(5{a^2} – 10ab + 15a\) jest równe iloczynowi
Układ równań \(\left\{ {\begin{array}{*{20}{c}}{4x + 2y = 10}\\{6x + ay = 15}\end{array}} \right.\) ma nieskończenie wiele rozwiązań, jeśli
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Rozwiązanie równania x(x + 3)- 49 = x(x – 4) należy do przedziału
Najmniejszą liczbą całkowitą należącą do zbioru rozwiązań nierówności \(\frac{3}{8} + \frac{x}{6} < \frac{{5x}}{{12}}\) jest
Wskaż, który zbiór przedstawiony na osi liczbowej jest zbiorem liczb spełniających jednocześnie następujące nierówności: \(3\left( {x – 1} \right)\left( {x – 5} \right){\rm{ }} \le {\rm{ }}0{\rm{ }}\;\;i\;\;x > 1.\)
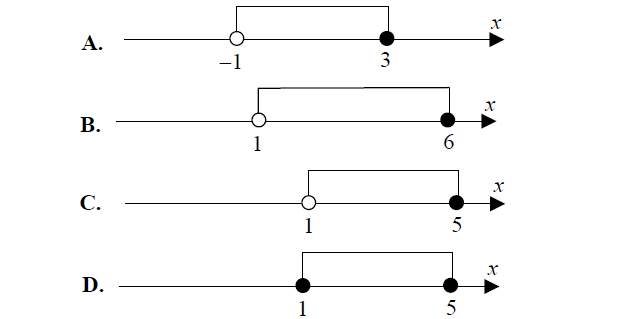 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Wyrażenie log4(2x-1) jest określone dla wszystkich liczb x spełniających warunek
Dane są funkcje liniowe f(x) = x – 2 oraz g(x) = x + 4 określone dla wszystkich liczb rzeczywistych x . Wskaż, który z poniższych wykresów jest wykresem funkcji h(x) = f(x)·g(x).
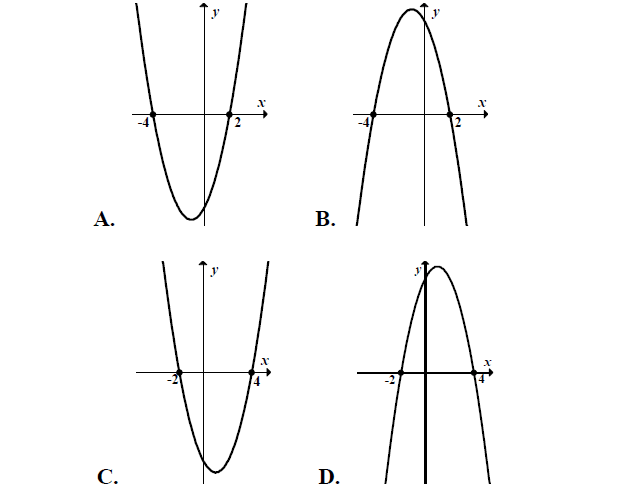 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Funkcja liniowa określona jest wzorem \(f\left( x \right) = – \sqrt 2 x + 4\). Miejscem zerowym tej funkcji jest liczba
Dany jest nieskończony ciąg geometryczny (an), w którym \({a_3} = 1\quad i\quad {a_4} = \frac{2}{3}\). Wtedy
Dany jest nieskończony rosnący ciąg arytmetyczny (an) o wyrazach dodatnich. Wtedy
Kąt \(\alpha \) jest ostry i \(\cos \;\alpha = \frac{5}{{13}}\). Wtedy
Wartość wyrażenia \(\frac{{{{\sin }^2}{{38}^ \circ } + {{\cos }^2}{{38}^ \circ } – 1}}{{{{\sin }^2}{{52}^ \circ } + {{\cos }^2}{{52}^ \circ } + 1}}\) jest równa
W prostopadłościanie ABCDEFGH mamy: |AB| = 5 , |AD| = 4 , |AE| = 3. Który z odcinków AB, BG, GE, EB jest najdłuższy?
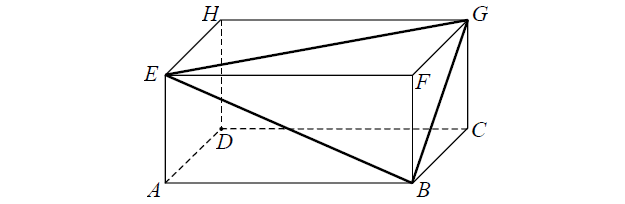
Punkt O jest środkiem okręgu. Kąt wpisany \(\alpha\) ma miarę
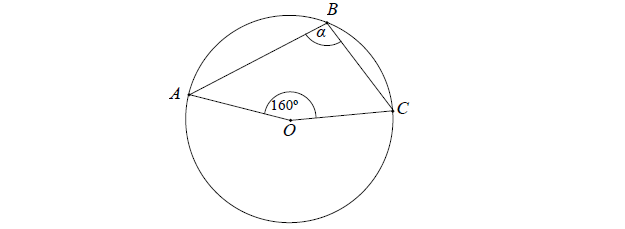
Wysokość rombu o boku długości 6 i kącie ostrym 60° jest równa
Prosta k ma równanie y = 2x – 3 . Wskaż równanie prostej l równoległej do prostej k i przechodzącej przez punkt D o współrzędnych (-2,1) .
Styczną do okręgu (x – 1)2 + y2 – 4 = 0 jest prosta o równaniu
Pole powierzchni całkowitej sześcianu jest równe 54. Długość przekątnej tego sześcianu jest równa
Objętość stożka o wysokości 8 i średnicy podstawy 12 jest równa
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Prawdopodobieństwo otrzymania sumy oczek równej trzy wynosi
Uczniowie pewnej klasy zostali poproszeni o odpowiedź na pytanie: „Ile osób liczy twoja rodzina?” Wyniki przedstawiono w tabeli:

Średnia liczba osób w rodzinie dla uczniów tej klasy jest równa 4. Wtedy liczba x jest równa
Rozwiąż nierówność \(3{x^2} – 10x + 3 \le 0\)
Treść dostępna po opłaceniu abonamentu.Uzasadnij, że jeżeli \(a + b = 1\quad i\quad {a^2} + {b^2} = 7,\quad to\quad {a^4} + {b^4} = 31\)
Treść dostępna po opłaceniu abonamentu.Na rysunku przedstawiono wykres funkcji f.
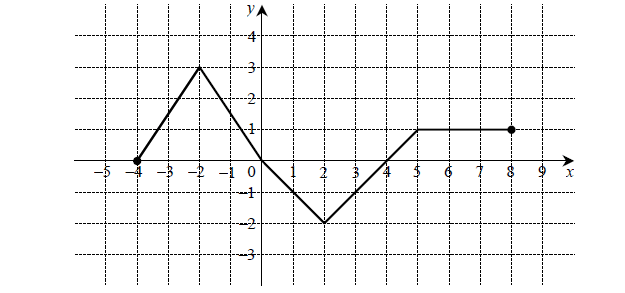
Odczytaj z wykresu i zapisz:
a) zbiór wartości funkcji f,
b) przedział maksymalnej długości, w którym funkcja f jest malejąca.
Treść dostępna po opłaceniu abonamentu.Liczby x, y, 19 w podanej kolejności tworzą ciąg arytmetyczny, przy czym x + y = 8 . Oblicz x i y.
Treść dostępna po opłaceniu abonamentu.Kąt \(\alpha \) jest ostry i \(\frac{{\sin \alpha }}{{\cos \alpha }} + \frac{{\cos \alpha }}{{\sin \alpha }} = 2.\) Oblicz wartość wyrażenia \(\sin \alpha \cdot \cos \alpha .\)
Treść dostępna po opłaceniu abonamentu.Dany jest czworokąt ABCD, w którym AB||CD . Na boku BC wybrano taki punkt E, że |EC| = |CD| i |EB| = |BA| . Wykaż, że kąt AED jest prosty.
Treść dostępna po opłaceniu abonamentu.Ze zbioru liczb {1, 2, 3,…, 7} losujemy kolejno dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo wylosowania liczb, których suma jest podzielna przez 3.
Treść dostępna po opłaceniu abonamentu.Okrąg o środku w punkcie S = (3,7) jest styczny do prostej o równaniu y = 2x – 3. Oblicz współrzędne punktu styczności.
Treść dostępna po opłaceniu abonamentu.Pewien turysta pokonał trasę 112 km, przechodząc każdego dnia tę samą liczbę kilometrów. Gdyby mógł przeznaczyć na tę wędrówkę o 3 dni więcej, to w ciągu każdego dnia mógłby przechodzić o 12 km mniej. Oblicz, ile kilometrów dziennie przechodził ten turysta.
Treść dostępna po opłaceniu abonamentu.Punkty K, L i M są środkami krawędzi BC, GH i AE sześcianu ABCDEFGH o krawędzi długości 1 (zobacz rysunek). Oblicz pole trójkąta KLM.
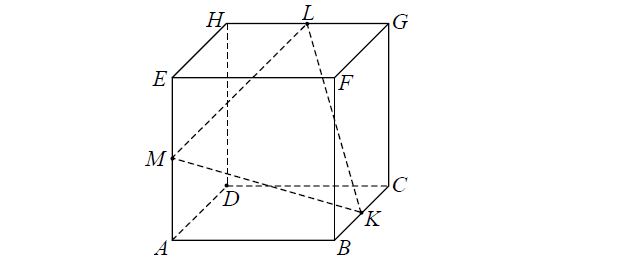 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
- Matura z matematyki 2017 – Maj podstawowa
- Matura z matematyki 2016 – Maj podstawowa
- Matura z matematyki 2015 – Maj podstawowa
- Matura z matematyki 2014 – Maj podstawowa
- Matura z matematyki 2013 – Maj podstawowa
- Matura z matematyki 2012 – Maj podstawowa
- Matura z matematyki 2011 – Maj podstawowa
- Matura z matematyki 2010 – Maj podstawowa
- Matura z matematyki 2009 – Maj podstawowa
- Matura z matematyki 2008 – Maj podstawowa
- Matura z matematyki 2007 – Maj podstawowa
- Matura z matematyki 2006 – Maj podstawowa
- Matura z matematyki 2005 – Maj podstawowa
- Matura z matematyki 2003 – Maj podstawowa




