Matura z matematyki 2012 – Czerwiec podstawowa
Zobacz arkusz i odpowiedzi z czerwcowej matury z matematyki 2012 online. Dokonaj szczegółowej analizy zadań, gdyż matematyka nie lubi pośpiechu!
Arkusz i odpowiedzi Centralnej Komisji Edukacyjnej
- Matura z matematyki czerwiec 2012 – Poziom Podstawowy – Arkusz CKE
- Matura z matematyki czerwiec 2012 – Poziom Podstawowy – Odpowiedzi CKE
Zadania maturalne są bardzo dobrym materiałem treningowym przed kolejnym, zbliżającym się egzaminem maturalnym. Zobacz odpowiedzi już teraz online!
Matura z matematyki czerwiec 2012 – Zadania i odpowiedzi
Ułamek \(\frac{{\sqrt 5 + 2}}{{\sqrt 5 – 2}}\) jest równy
Liczbami spełniającymi równanie |2x + 3| = 5 są
Równanie \((x + 5)(x – 3)({x^2} + 1) = 0\) ma
Marża równa 1,5% kwoty pożyczonego kapitału była równa 3000 zł. Wynika stąd, że pożyczono
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
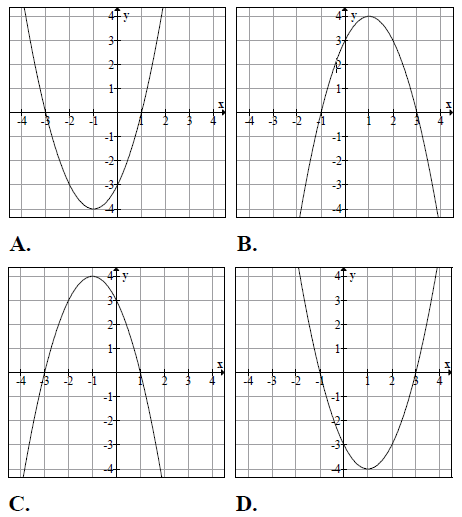
Na jednym z poniższych rysunków przedstawiono fragment wykresu funkcji \(y = {x^2} + 2x – 3\) . Wskaż ten rysunek.
 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Wierzchołkiem paraboli będącej wykresem funkcji określonej wzorem \(y = {x^2} – 4x + 4\) jest punkt o współrzędnych
Jeden kąt trójkąta ma miarę 54°. Z pozostałych dwóch kątów tego trójkąta jeden jest 6 razy większy od drugiego. Miary pozostałych kątów są równe
Krótszy bok prostokąta ma długość 6. Kąt między przekątną prostokąta i dłuższym bokiem ma miarę 30° . Dłuższy bok prostokąta ma długość
Cięciwa okręgu ma długość 8 cm i jest oddalona od jego środka o 3 cm. Promień tego okręgu ma długość
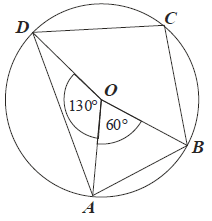
Punkt O jest środkiem okręgu. Kąt wpisany BAD ma miarę
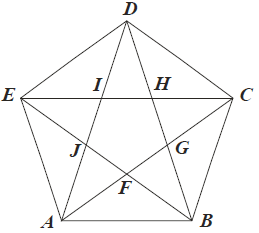
Pięciokąt ABCDE jest foremny. Wskaż trójkąt przystający do trójkąta ECD
Punkt O jest środkiem okręgu przedstawionego na rysunku. Równanie tego okręgu ma postać:
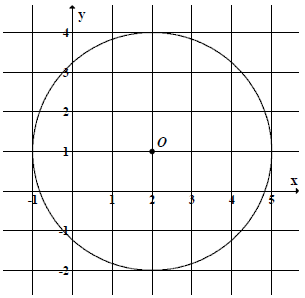
Wyrażenie \(\frac{{3x + 1}}{{x – 2}} – \frac{{2x – 1}}{{x + 3}}\) jest równe
Ciąg \(({a_n})\) jest określony wzorem \({a_n} = \sqrt {2n + 4} \quad dla\quad n \ge 1\). Wówczas
Ciąg \(\left( {2\sqrt 2 ,\,4,\,a} \right)\) jest geometryczny. Wówczas
Kąt \(\alpha\) jest ostry i \(tg\alpha = 1\). Wówczas
Wiadomo, że dziedziną funkcji f określonej wzorem \(f(x) = \frac{{x – 7}}{{2x + a}}\) jest zbiór \(( – \infty ,2) \cup (2, + \infty )\). Wówczas
Jeden z rysunków przedstawia wykres funkcji liniowej f(x) = ax + b , gdzie a > 0 i b < 0 . Wskaż ten wykres.
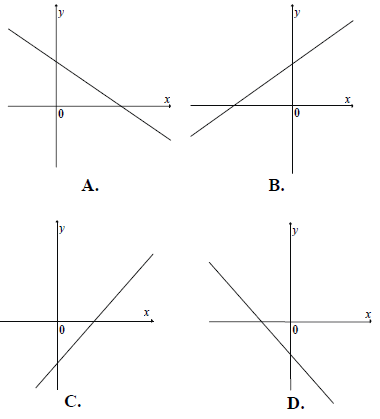 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Punkt S = (2,7) jest środkiem odcinka AB, w którym A = (-1,3) . Punkt B ma współrzędne:
W kolejnych sześciu rzutach kostką otrzymano następujące wyniki: 6, 3, 1, 2, 5, 5. Mediana tych wyników jest równa:
Równość \({(a + 2\sqrt 2 )^2} = {a^2} + 28\sqrt 2 + 8\) zachodzi dla
Trójkąt prostokątny o przyprostokątnych 4 i 6 obracamy wokół dłuższej przyprostokątnej. Objętość powstałego stożka jest równa
Jeżeli A i B są zdarzeniami losowymi, B’ jest zdarzeniem przeciwnym do B, P(A)=0,3 , P(B’)=0,4 oraz P(A∩B)=∅ to P(A∪B) jest równe
Przekrój osiowy walca jest kwadratem o boku a. Jeżeli r oznacza promień podstawy walca, h oznacza wysokość walca, to
Rozwiąż nierówność \({x^2} – 3x – 10 < 0\) Treść dostępna po opłaceniu abonamentu.
Średnia wieku w pewnej grupie studentów jest równa 23 lata. Średnia wieku tych studentów i ich opiekuna jest równa 24 lata. Opiekun ma 39 lat. Oblicz, ilu studentów jest w tej grupie.
Treść dostępna po opłaceniu abonamentu.Podstawy trapezu prostokątnego mają długości 6 i 10 oraz tangens jego kąta ostrego jest równy 3. Oblicz pole tego trapezu.
Treść dostępna po opłaceniu abonamentu.Uzasadnij, że jeżeli \(\alpha\) jest kątem ostrym, to \({\sin ^4}\alpha + {\cos ^2}\alpha = {\sin ^2}\alpha + {\cos ^4}\alpha \).
Treść dostępna po opłaceniu abonamentu.Uzasadnij, że suma kwadratów trzech kolejnych liczb całkowitych przy dzieleniu przez 3 daje resztę 2.
Treść dostępna po opłaceniu abonamentu.Suma \({S_n} = {a_1} + {a_2} + … + {a_n}\) początkowych n wyrazów pewnego ciągu arytmetycznego \(({a_n})\) jest określona wzorem \({S_n} = {n^2} – 2n\;\;dla\;\;n \ge 1\). Wyznacz wzór na n – ty wyraz tego ciągu.
Treść dostępna po opłaceniu abonamentu.Dany jest romb, którego kąt ostry ma miarę 45°, a jego pole jest równe \(50\sqrt 2 \). Oblicz wysokość tego rombu.
Treść dostępna po opłaceniu abonamentu.Punkty A=(2,11), B(8,23), C(6,14) są wierzchołkami trójkąta. Wysokość trójkąta poprowadzona z wierzchołka C przecina prostą AB w punkcie D. Oblicz współrzędne punktu D.
Treść dostępna po opłaceniu abonamentu.Oblicz, ile jest liczb naturalnych pięciocyfrowych, w zapisie których nie występuje zero, jest dokładnie jedna cyfra 7 i dokładnie jedna cyfra parzysta.
Treść dostępna po opłaceniu abonamentu.Arkusz i odpowiedzi Centralnej Komisji Edukacyjnej
- Matura z matematyki czerwiec 2012 – Poziom Podstawowy – Arkusz CKE
- Matura z matematyki czerwiec 2012 – Poziom Podstawowy – Odpowiedzi CKE
Zadania maturalne są bardzo dobrym materiałem treningowym przed kolejnym, zbliżającym się egzaminem maturalnym. Zobacz odpowiedzi już teraz online!
Matura z matematyki czerwiec 2012 – Zadania i odpowiedzi
Ułamek \(\frac{{\sqrt 5 + 2}}{{\sqrt 5 – 2}}\) jest równy
Liczbami spełniającymi równanie |2x + 3| = 5 są
Równanie \((x + 5)(x – 3)({x^2} + 1) = 0\) ma
Marża równa 1,5% kwoty pożyczonego kapitału była równa 3000 zł. Wynika stąd, że pożyczono
Na jednym z poniższych rysunków przedstawiono fragment wykresu funkcji \(y = {x^2} + 2x – 3\) . Wskaż ten rysunek.
 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Wierzchołkiem paraboli będącej wykresem funkcji określonej wzorem \(y = {x^2} – 4x + 4\) jest punkt o współrzędnych
Jeden kąt trójkąta ma miarę 54°. Z pozostałych dwóch kątów tego trójkąta jeden jest 6 razy większy od drugiego. Miary pozostałych kątów są równe
Krótszy bok prostokąta ma długość 6. Kąt między przekątną prostokąta i dłuższym bokiem ma miarę 30° . Dłuższy bok prostokąta ma długość
Cięciwa okręgu ma długość 8 cm i jest oddalona od jego środka o 3 cm. Promień tego okręgu ma długość
Punkt O jest środkiem okręgu. Kąt wpisany BAD ma miarę

Pięciokąt ABCDE jest foremny. Wskaż trójkąt przystający do trójkąta ECD

Punkt O jest środkiem okręgu przedstawionego na rysunku. Równanie tego okręgu ma postać:
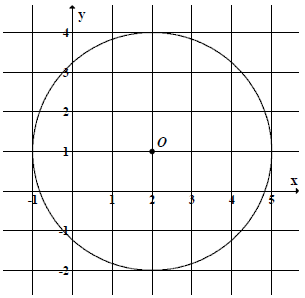
Wyrażenie \(\frac{{3x + 1}}{{x – 2}} – \frac{{2x – 1}}{{x + 3}}\) jest równe
Ciąg \(({a_n})\) jest określony wzorem \({a_n} = \sqrt {2n + 4} \quad dla\quad n \ge 1\). Wówczas
Ciąg \(\left( {2\sqrt 2 ,\,4,\,a} \right)\) jest geometryczny. Wówczas
Kąt \(\alpha\) jest ostry i \(tg\alpha = 1\). Wówczas
Wiadomo, że dziedziną funkcji f określonej wzorem \(f(x) = \frac{{x – 7}}{{2x + a}}\) jest zbiór \(( – \infty ,2) \cup (2, + \infty )\). Wówczas
Jeden z rysunków przedstawia wykres funkcji liniowej f(x) = ax + b , gdzie a > 0 i b < 0 . Wskaż ten wykres.
 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Punkt S = (2,7) jest środkiem odcinka AB, w którym A = (-1,3) . Punkt B ma współrzędne:
W kolejnych sześciu rzutach kostką otrzymano następujące wyniki: 6, 3, 1, 2, 5, 5. Mediana tych wyników jest równa:
Równość \({(a + 2\sqrt 2 )^2} = {a^2} + 28\sqrt 2 + 8\) zachodzi dla
Trójkąt prostokątny o przyprostokątnych 4 i 6 obracamy wokół dłuższej przyprostokątnej. Objętość powstałego stożka jest równa
Jeżeli A i B są zdarzeniami losowymi, B’ jest zdarzeniem przeciwnym do B, P(A)=0,3 , P(B’)=0,4 oraz P(A∩B)=∅ to P(A∪B) jest równe
Przekrój osiowy walca jest kwadratem o boku a. Jeżeli r oznacza promień podstawy walca, h oznacza wysokość walca, to
Rozwiąż nierówność \({x^2} – 3x – 10 < 0\)
Treść dostępna po opłaceniu abonamentu.Średnia wieku w pewnej grupie studentów jest równa 23 lata. Średnia wieku tych studentów i ich opiekuna jest równa 24 lata. Opiekun ma 39 lat. Oblicz, ilu studentów jest w tej grupie.
Treść dostępna po opłaceniu abonamentu.Podstawy trapezu prostokątnego mają długości 6 i 10 oraz tangens jego kąta ostrego jest równy 3. Oblicz pole tego trapezu.
Treść dostępna po opłaceniu abonamentu.Uzasadnij, że jeżeli \(\alpha\) jest kątem ostrym, to \({\sin ^4}\alpha + {\cos ^2}\alpha = {\sin ^2}\alpha + {\cos ^4}\alpha \).
Uzasadnij, że suma kwadratów trzech kolejnych liczb całkowitych przy dzieleniu przez 3 daje resztę 2.
Treść dostępna po opłaceniu abonamentu.Suma \({S_n} = {a_1} + {a_2} + … + {a_n}\) początkowych n wyrazów pewnego ciągu arytmetycznego \(({a_n})\) jest określona wzorem \({S_n} = {n^2} – 2n\;\;dla\;\;n \ge 1\). Wyznacz wzór na n – ty wyraz tego ciągu.
Treść dostępna po opłaceniu abonamentu.Dany jest romb, którego kąt ostry ma miarę 45°, a jego pole jest równe \(50\sqrt 2 \). Oblicz wysokość tego rombu.
Treść dostępna po opłaceniu abonamentu.Punkty A=(2,11), B(8,23), C(6,14) są wierzchołkami trójkąta. Wysokość trójkąta poprowadzona z wierzchołka C przecina prostą AB w punkcie D. Oblicz współrzędne punktu D.
Treść dostępna po opłaceniu abonamentu.Oblicz, ile jest liczb naturalnych pięciocyfrowych, w zapisie których nie występuje zero, jest dokładnie jedna cyfra 7 i dokładnie jedna cyfra parzysta.
Treść dostępna po opłaceniu abonamentu.Dany jest graniastosłup prawidłowy trójkątny ABCDEF o podstawach ABC i DEF i krawędziach bocznych AD, BE i CF (zobacz rysunek). Długość krawędzi podstawy AB jest równa 8, a pole trójkąta ABF jest równe 52. Oblicz objętość tego graniastosłupa.
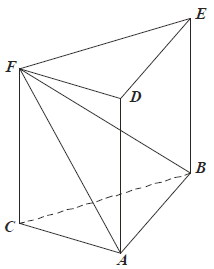 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
- Matura z matematyki 2017 – Maj podstawowa
- Matura z matematyki 2016 – Maj podstawowa
- Matura z matematyki 2015 – Maj podstawowa
- Matura z matematyki 2014 – Maj podstawowa
- Matura z matematyki 2013 – Maj podstawowa
- Matura z matematyki 2012 – Maj podstawowa
- Matura z matematyki 2011 – Maj podstawowa
- Matura z matematyki 2010 – Maj podstawowa
- Matura z matematyki 2009 – Maj podstawowa
- Matura z matematyki 2008 – Maj podstawowa
- Matura z matematyki 2007 – Maj podstawowa
- Matura z matematyki 2006 – Maj podstawowa
- Matura z matematyki 2005 – Maj podstawowa
- Matura z matematyki 2003 – Maj podstawowa




