Matura z matematyki 2010 – Maj podstawowy
Matura z matematyki 2010 na poziomie podstawowym stała się faktem. Zobacz arkusze i odpowiedzi do zadań maturalnych online.
Arkusz i odpowiedzi Centralnej Komisji Edukacyjnej
- Matura z matematyki 2010 – Maj Poziom Podstawowy – Arkusz CKE
- Matura z matematyki 2010 – Maj Poziom Podstawowy – Odpowiedzi CKE
Warto zapamiętać!
- Niektóre zadania maturalne i działy matematyczne co roku pojawiają się na maturze z matematyki!
Skutecznym środkiem i najlepszym treningiem do zdania egzaminu maturalnego z matematyki jest nauka do matury na podstawie arkuszów maturalnych z poprzednich lat!
Matura z matematyki 2010 – zadania i odpowiedzi online
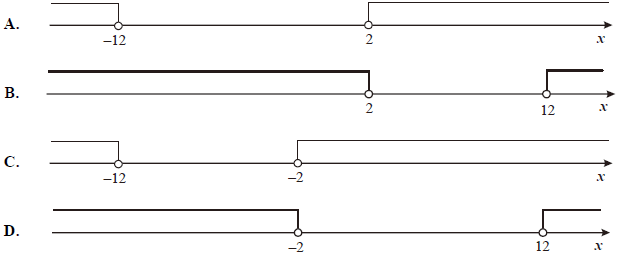
Wskaż rysunek, na którym jest przedstawiony zbiór rozwiązań nierówności |x + 7| > 5 .
Spodnie po obniżce ceny o 30% kosztują 126 zł. Ile kosztowały spodnie przed obniżką?
Liczba \({\left( {\frac{{{2^{ – 2}} \cdot {3^{ – 1}}}}{{{2^{ – 1}} \cdot {3^{ – 2}}}}} \right)^0}\) jest równa
Liczba \({\log _4}8 + {\log _4}2\) jest równa
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Dane są wielomiany \(W\left( x \right) = – 2{x^3} + 5{x^2} – 3\quad oraz\quad P\left( x \right) = 2{x^3} + 12x.\) Wielomian \(W\left( x \right){\rm{ }} + P\left( x \right)\) jest równy
Rozwiązaniem równania \(\frac{{3x – 1}}{{7x + 1}} = \frac{2}{5}\)jest
Do zbioru rozwiązań nierówności (x – 2)(x + 3) < 0 należy liczba
Wykresem funkcji kwadratowej \(f\left( x \right) = – 3{x^2} + 3\) jest parabola o wierzchołku w punkcie
Prosta o równaniu y = -2x + (3m+ 3) przecina w układzie współrzędnych oś Oy w punkcie (0, 2) . Wtedy
Na rysunku jest przedstawiony wykres funkcji y = f (x) .
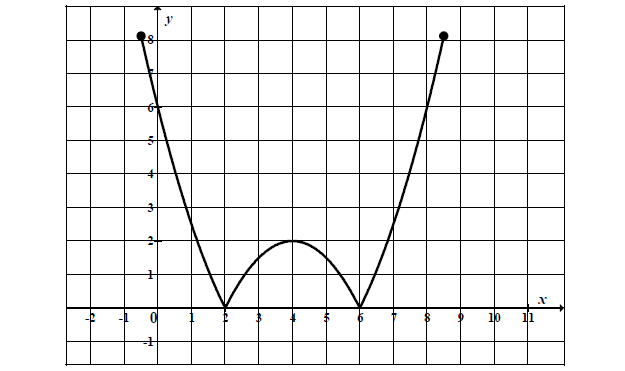
Które równanie ma dokładnie trzy rozwiązania?
W ciągu arytmetycznym \(\left( {{a_n}} \right)\) dane są: \({a_3} = 13\quad i\quad {a_5} = 39.\) Wtedy wyraz \(a{\;_1}\) jest równy
W ciągu geometrycznym \(\left( {{a_n}} \right)\) dane są: \({a_1} = 3\quad i\quad {a_4} = 24.\) Iloraz tego ciągu jest równy
Liczba przekątnych siedmiokąta foremnego jest równa
Kąt \(\alpha\) jest ostry i \(\sin \alpha = \frac{3}{4}\). Wartość wyrażenia \(2 – {\cos ^2}\alpha \) jest równa
Okrąg opisany na kwadracie ma promień 4. Długość boku tego kwadratu jest równa
Podstawa trójkąta równoramiennego ma długość 6, a ramię ma długość 5. Wysokość opuszczona na podstawę ma długość
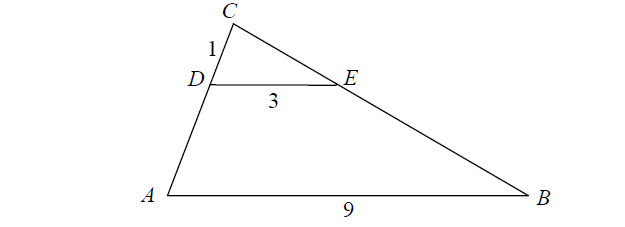
Odcinki AB i DE są równoległe. Długości odcinków CD, DE i AB są odpowiednio równe 1, 3 i 9. Długość odcinka AD jest równa
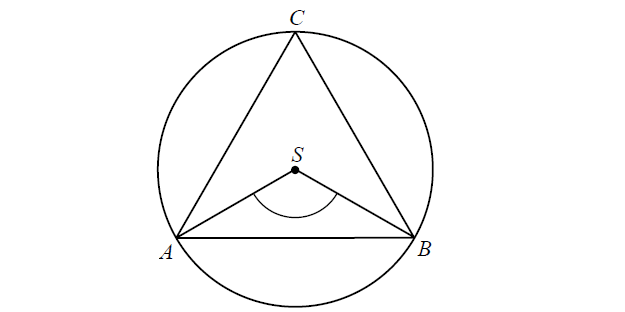
Punkty A, B, C leżące na okręgu o środku S są wierzchołkami trójkąta równobocznego. Miara zaznaczonego na rysunku kąta środkowego ASB jest równa
Latawiec ma wymiary podane na rysunku. Powierzchnia zacieniowanego trójkąta jest równa
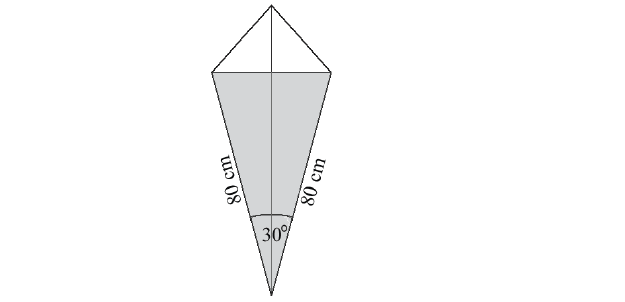
Współczynnik kierunkowy prostej równoległej do prostej o równaniu y = -3x + 5 jest równy:
Wskaż równanie okręgu o promieniu 6.
Punkty A = (-5, 2) i B = (3,-2) są wierzchołkami trójkąta równobocznego ABC. Obwód tego trójkąta jest równy
Pole powierzchni całkowitej prostopadłościanu o wymiarach 5×3×4 jest równe
Ostrosłup ma 18 wierzchołków. Liczba wszystkich krawędzi tego ostrosłupa jest równa
Średnia arytmetyczna dziesięciu liczb x, 3, 1, 4, 1, 5, 1, 4, 1, 5 jest równa 3. Wtedy
Rozwiąż nierówność \({x^2} – x – 2 \le 0\)
Treść dostępna po opłaceniu abonamentu.Rozwiąż równanie \({x^3} – 7{x^2} – 4x + 28 = 0\)
Treść dostępna po opłaceniu abonamentu.Trójkąty prostokątne równoramienne ABC i CDE są położone tak, jak na poniższym rysunku (w obu trójkątach kąt przy wierzchołku C jest prosty). Wykaż, że |AD| = |BE| .
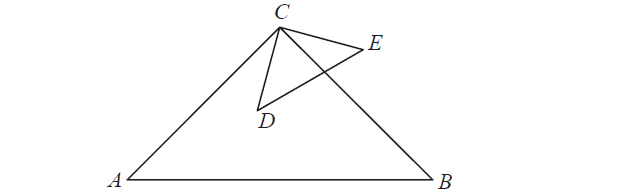 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Kąt \(\alpha \) jest ostry i \(tg\alpha = \frac{5}{{12}}\) Oblicz \(\cos \alpha .\)
Treść dostępna po opłaceniu abonamentu.Wykaż, że jeśli a > 0 , to \(\frac{{{a^2} + 1}}{{a + 1}} \ge \frac{{a + 1}}{2}\)
Treść dostępna po opłaceniu abonamentu.W trapezie prostokątnym krótsza przekątna dzieli go na trójkąt prostokątny i trójkąt równoboczny. Dłuższa podstawa trapezu jest równa 6. Oblicz obwód tego trapezu.
Treść dostępna po opłaceniu abonamentu.Podstawą ostrosłupa ABCD jest trójkąt ABC. Krawędź AD jest wysokością ostrosłupa (zobacz rysunek). Oblicz objętość ostrosłupa ABCD, jeśli wiadomo, że |AD| =12 , |BC| = 6 , |BD| = |CD| =13.
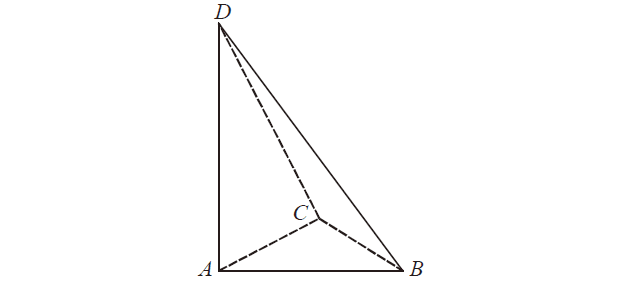 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Doświadczenie losowe polega na dwukrotnym rzucie symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia A polegającego na tym, że w pierwszym rzucie otrzymamy parzystą liczbę oczek i iloczyn liczb oczek w obu rzutach będzie podzielny przez 12. Wynik przedstaw w postaci ułamka zwykłego nieskracalnego.
Treść dostępna po opłaceniu abonamentu.W dwóch hotelach wybudowano prostokątne baseny. Basen w pierwszym hotelu ma powierzchnię 240 m2. Basen w drugim hotelu ma powierzchnię 350 m2 oraz jest o 5 m dłuższy i 2 m szerszy niż w pierwszym hotelu. Oblicz, jakie wymiary mogą mieć baseny w obu hotelach. Podaj wszystkie możliwe odpowiedzi.
Treść dostępna po opłaceniu abonamentu.- Matura z matematyki 2017 – Maj podstawowa
- Matura z matematyki 2016 – Maj podstawowa
- Matura z matematyki 2015 – Maj podstawowa
- Matura z matematyki 2014 – Maj podstawowa
- Matura z matematyki 2013 – Maj podstawowa
- Matura z matematyki 2012 – Maj podstawowa
- Matura z matematyki 2011 – Maj podstawowa
- Matura z matematyki 2010 – Maj podstawowa
- Matura z matematyki 2009 – Maj podstawowa
- Matura z matematyki 2008 – Maj podstawowa
- Matura z matematyki 2007 – Maj podstawowa
- Matura z matematyki 2006 – Maj podstawowa
- Matura z matematyki 2005 – Maj podstawowa
- Matura z matematyki 2003 – Maj podstawowa




