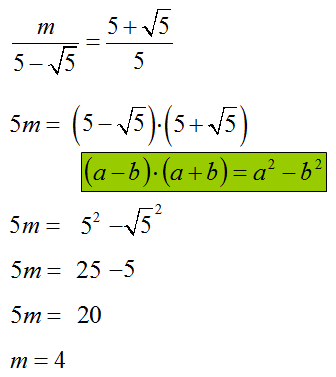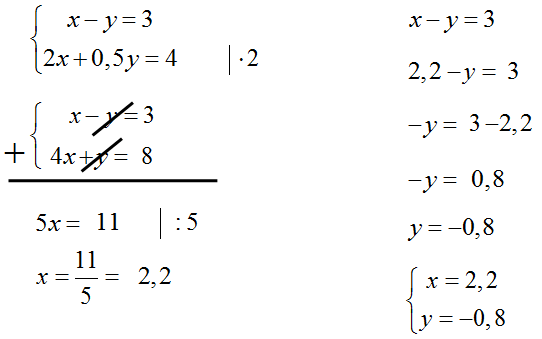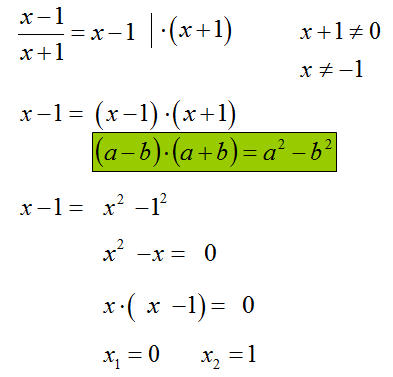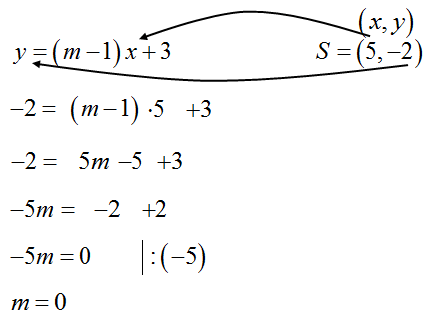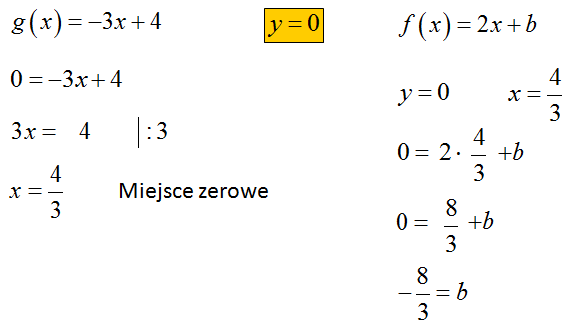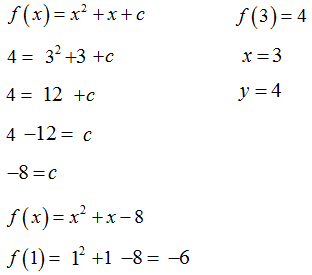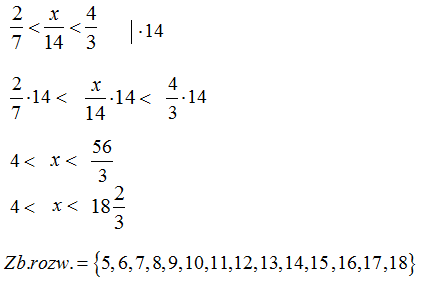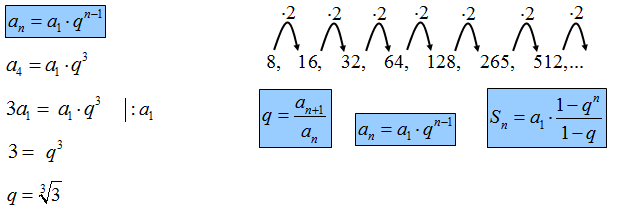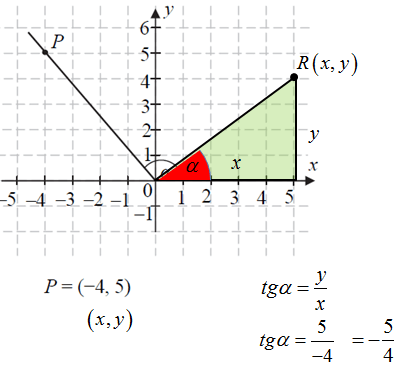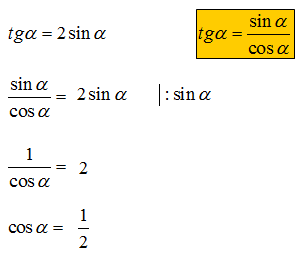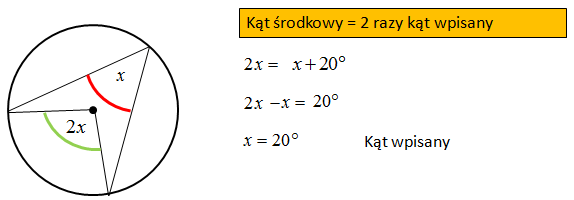Matura z matematyki 2015 – Maj podstawowa
Majowa matura z matematyki 2015 na poziomie podstawowym przechodzi do historii. Zobacz arkusz i wszystkie odpowiedzi do zadań w postaci rozwiązań video. Będzie to jednocześnie solidna powtórka dla przyszłorocznych maturzystów.
Arkusz i odpowiedzi Centralnej Komisji Egzaminacyjnej
- Matura z matematyki 2015 – Maj Poziom Podstawowy – Arkusz CKE
Matura z matematyki 2015 – zadania i odpowiedzi online
Wskaż rysunek, na którym przedstawiono przedział, będący zbiorem wszystkich rozwiązań nierówności −4≤x−1≤4.
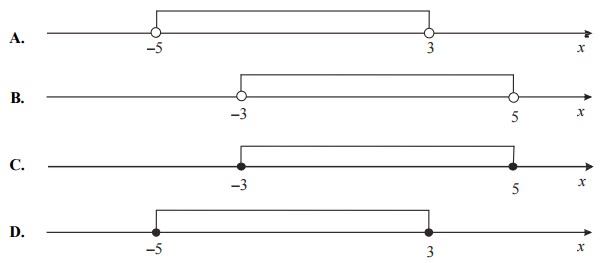
Odpowiedź: C.
Wskazówka: Można dodawać lub odejmować liczby całkowite do stron nierówności. \[\begin{align} & -4\le x-1\le 4\quad \left| +1 \right. \\ & -3\le x\le 5 \\ \end{align}\]
Dane są liczby \(a=-\frac{1}{27},\ b={{\log }_{\frac{1}{4}}}64,\ c={{\log }_{\frac{1}{3}}}27\). Iloczyn abc jest równy
Odpowiedź: B.
Najlepiej zastosować definicję logarytmu i oddzielnie obliczyć wartości poszczególnych logarytmów.
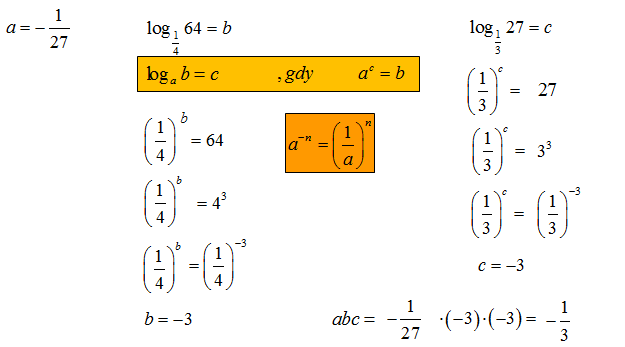
Kwotę 1000 zł ulokowano w banku na roczną lokatę oprocentowaną w wysokości 4% w stosunku rocznym. Po zakończeniu lokaty od naliczonych odsetek odprowadzany jest podatek w wysokości 19%. Maksymalna kwota, jaką po upływie roku będzie można wypłacić z banku jest równa
Odpowiedź: C.
\(1000\cdot \frac{4}{100}\cdot \frac{19}{100}\) – Pieniądze zabrane jako podatek
\(1000\cdot \frac{4}{100}\cdot \frac{81}{100}\) – Pieniądze po odprowadzeniu podatku – zysk- odsetki
\(1000+1000\cdot \frac{4}{100}\cdot \frac{81}{100}=1000\cdot \left( \begin{matrix}
{} \\
{} \\
\end{matrix} \right.1\left. +\frac{4}{100}\cdot \frac{81}{100} \right)\) –
Kapitał + odsetki = Kwota możliwa do wypłaty
Równość \(\frac{m}{5-\sqrt{5}}=\frac{5+\sqrt{5}}{5}\) zachodzi dla
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Odpowiedź: B.
Układ równań \(\left\{ \begin{matrix} x-y=3 \\ 2x+0,5y=4 \\ \end{matrix} \right.\) opisuje w układzie współrzędnych na płaszczyźnie
Odpowiedź: B.
Suma wszystkich pierwiastków równania (x + 3)(x + 7)(x −11) = 0 jest równa
Odpowiedź: C.
\[\begin{align} & \left( x+3 \right)\,\left( x+7 \right)\,\left( x-11 \right)=0 \\ & {{x}_{1}}=-3\quad {{x}_{2}}=-7\quad {{x}_{3}}=11 \\ & Suma=-3+\left( -7 \right)+11=1 \\ \end{align}\]
Równanie \(\frac{x-1}{x+1}=x-1\)
Odpowiedź: D.
Na rysunku przedstawiono wykres funkcji f. Zbiorem wartości funkcji f jest
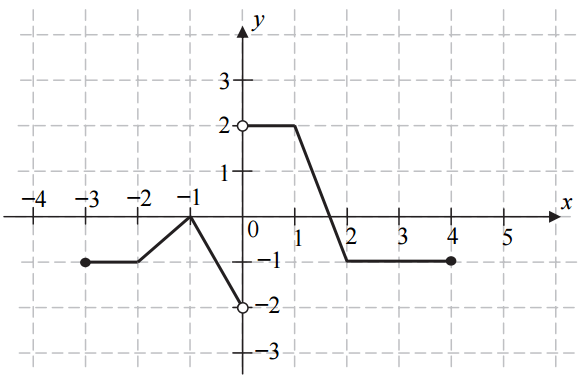
Odpowiedź: D.
Na wykresie funkcji liniowej określonej wzorem f(x)=(m−1)x+3 leży punkt S=(5,−2). Zatem
Odpowiedź: B.
Funkcja liniowa f określona wzorem f(x)=2x+b ma takie samo miejsce zerowe, jakie ma funkcja liniowa g(x)=−3x+4. Stąd wynika, że
Odpowiedź: C.
Funkcja kwadratowa określona jest wzorem f(x)=x2+x+c. Jeżeli f(3)=4, to
Odpowiedź: A.
Ile liczb całkowitych x spełnia nierówność \[\frac{2}{7}<\frac{x}{14}<\frac{4}{3}\]
Odpowiedź: A.
W rosnącym ciągu geometrycznym (an), określonym dla n ≥ 1, spełniony jest warunek a4=3a3. Iloraz q tego ciągu jest równy
Odpowiedź: C.
Tangens kąta α zaznaczonego na rysunku jest równy
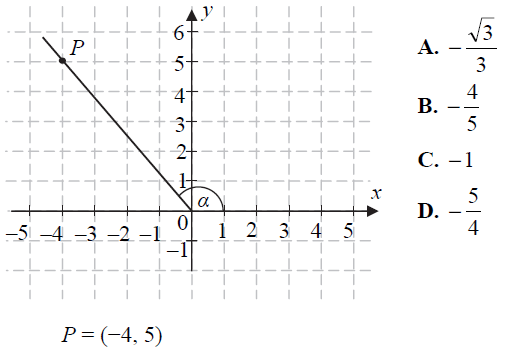 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Odpowiedź: D.
Jeżeli 0°<α<90° oraz tgα=2sinα
Odpowiedź: A.
Miara kąt wpisanego w okrąg jest o o 20° mniejsza od miary kąta środkowego opartego na tym samym łuku. Wynika stąd, że miara kąta wpisanego jest równa.
Odpowiedź: C.
Pole rombu o obwodzie 8 jest równe 1. Kąt ostry tego rombu ma miarę α . Wtedy
Prosta l o równaniu y=m2x+3 jest równoległa do prostej k o równaniu y=(4m−4)x−3 .Zatem
Proste o równaniach: y=2mx−m2−1 oraz y=4m2x+m2+1 są prostopadłe dla
Dane są punkty M=(−2,1) i N=(−1,3) . Punkt K jest środkiem odcinka MN. Obrazem punktu K w symetrii względem początku układu współrzędnych jest punkt
W graniastosłupie prawidłowym czworokątnym EFGHIJKL wierzchołki E, G, L połączono odcinkami (tak jak na rysunku).
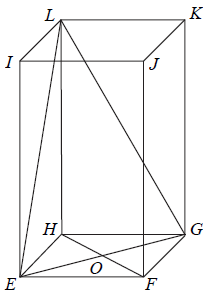
Wskaż kąt między wysokością OL trójkąta EGL i płaszczyzną podstawy tego graniastosłupa.
Przekrojem osiowym stożka jest trójkąt równoboczny o boku długości 6 . Objętość tego stożka jest równa
Każda krawędź graniastosłupa prawidłowego trójkątnego ma długość równą 8 . Pole powierzchni całkowitej tego graniastosłupa jest równe
Treść dostępna po opłaceniu abonamentu.Średnia arytmetyczna zestawu danych: 2, 4, 7, 8, 9 jest taka sama jak średnia arytmetyczna zestawu danych: 2, 4, 7, 8, 9, x. Wynika stąd, że
Treść dostępna po opłaceniu abonamentu.W każdym z trzech pojemników znajduje się para kul, z których jedna jest czerwona, a druga – niebieska. Z każdego pojemnika losujemy jedną kulę. Niech p oznacza prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie dwie z trzech wylosowanych kul będą czerwone. Wtedy
Treść dostępna po opłaceniu abonamentu.Wykaż, że dla każdej liczby rzeczywistej x i dla każdej liczby rzeczywistej y prawdziwa jest nierówność
Treść dostępna po opłaceniu abonamentu.Dany jest kwadrat ABCD. Przekątne AC i BD przecinają się w punkcie E. Punkty K i M są środkami odcinków – odpowiednio – AE i EC. Punkty L i N leżą na przekątnej BD tak, że ********************************(zobacz rysunek). Wykaż, że stosunek pola czworokąta KLMN do pola kwadratu ABCD jest równy 1: 3.
Treść dostępna po opłaceniu abonamentu.Oblicz najmniejszą i największą wartość funkcji kwadratowej
Treść dostępna po opłaceniu abonamentu.W układzie współrzędnych są dane punkty A = (−43,−12) , B = (50,19) . Prosta AB przecina oś Ox w punkcie P . Oblicz pierwszą współrzędną punktu P .
Treść dostępna po opłaceniu abonamentu.Jeżeli do licznika i do mianownika nieskracalnego dodatniego ułamka dodamy połowę jego licznika, to otrzymamy
Treść dostępna po opłaceniu abonamentu.Wysokość graniastosłupa prawidłowego czworokątnego jest równa 16 . Przekątna graniastosłupa jest nachylona do płaszczyzny jego podstawy pod kątem, którego cosinus jest równy
Treść dostępna po opłaceniu abonamentu.Wśród 115 osób przeprowadzono badania ankietowe, związane z zakupami w pewnym kiosku. W poniższej tabeli przedstawiono informacje o tym, ile osób kupiło bilety tramwajowe ulgowe oraz ile osób kupiło bilety tramwajowe normalne.
Treść dostępna po opłaceniu abonamentu.- Matura z matematyki 2017 – Maj podstawowa
- Matura z matematyki 2016 – Maj podstawowa
- Matura z matematyki 2015 – Maj podstawowa
- Matura z matematyki 2014 – Maj podstawowa
- Matura z matematyki 2013 – Maj podstawowa
- Matura z matematyki 2012 – Maj podstawowa
- Matura z matematyki 2011 – Maj podstawowa
- Matura z matematyki 2010 – Maj podstawowa
- Matura z matematyki 2009 – Maj podstawowa
- Matura z matematyki 2008 – Maj podstawowa
- Matura z matematyki 2007 – Maj podstawowa
- Matura z matematyki 2006 – Maj podstawowa
- Matura z matematyki 2005 – Maj podstawowa
- Matura z matematyki 2003 – Maj podstawowa