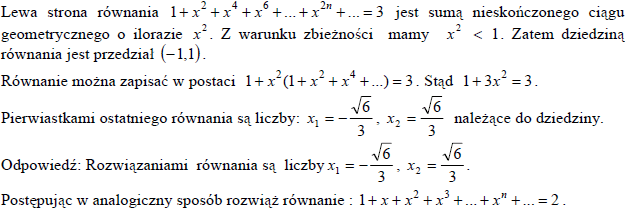Matura z matematyki 2003 – Maj podstawowa

Rysunek przedstawia fragment wykresu funkcji kwadratowej \(f.\)
a) Podaj miejsca zerowe funkcji \(f.\)
b) Podaj rozwiązania nierówności \(f\left( x \right) \le 0.\)
c) Podaj rozwiązania równania \(f\left( x \right) = 3.\)

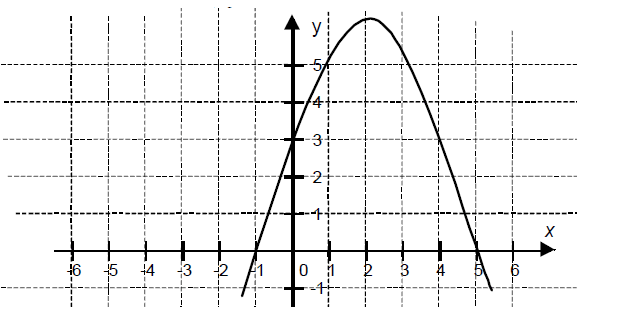
Dane dotyczące wzrostu chłopców z klasy II B przedstawione są na diagramie.
a) Oblicz średni wzrost chłopców z klasy II B (podaj wynik dokładny).
b) Ilu chłopców z klasy II B ma wzrost wyższy od średniego?

Liczby 102, 105, 108, 111,… są kolejnymi, początkowymi wyrazami pewnego ciągu arytmetycznego \(\left( {{a_n}} \right)\,.\) Zapisz wzór ogólny na n-ty wyraz tego ciągu. Oblicz wyraz \({a_{81}}\,.\)

Przed wejściem do przychodni lekarskiej znajdują się schody mające 8 stopni po 15 cm wysokości każdy. Postanowiono zbudować podjazd dla niepełnosprawnych o nachyleniu \(7^\circ .\) Oblicz długość podjazdu. Wynik podaj w zaokrągleniu do 10 cm.

Ciąg \(\left( {{a_n}} \right)\,\) określony jest wzorem \[\left\{ {\begin{array}{*{20}{c}} {{a_1} = 1\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad }\\ {{a_2} = 2\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad }\\ {{a_{n + 2}} = {2^{n – 1}} + {a_n} + {a_{n + 1}}\quad dla\quad n \in N\backslash \left\{ 0 \right\}} \end{array}} \right.\] Wyznacz czwarty wyraz tego ciąg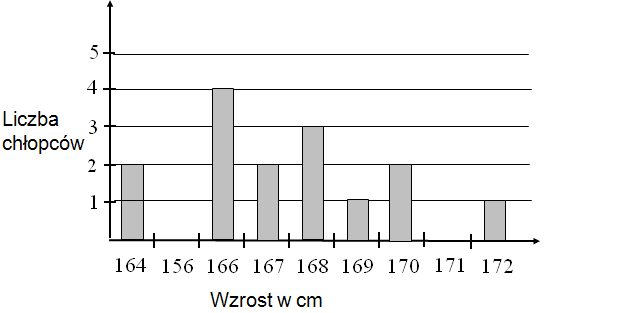u.

Rysunek przedstawia fragment wykresu funkcji liniowej f. Wykres funkcji g jest obrazem wykresu funkcji f otrzymanym za pomocą przesunięcia o wektor \(\overrightarrow u = \left[ {2,\,1} \right].\) Wyznacz miejsce zerowe funkcji g.

Składka na ubezpieczenie zdrowotne jest równa 7,5% podstawy wymiaru składek na ubezpieczenie społeczne. Podstawa wymiaru składek na ubezpieczenie społeczne jest równa 60% przeciętnego wynagrodzenia. Oblicz wysokość składki na ubezpieczenie zdrowotne przyjmując, że przeciętne wynagrodzenie jest równe 1869,76 zł. Wynik podaj w zaokrągleniu do 1 grosza.

Oblicz pole działki rekreacyjnej, której plan przedstawiony jest na rysunku. Zakładamy, że kąty ABC i ECD są kątami prostymi.

Kupując los loterii można wygrać nagrodę główną, którą jest zestaw płyt kompaktowych lub jedną z 10 nagród książkowych. Przy zakupie jednego losu prawdopodobieństwo wygrania nagrody książkowej jest równe \(\frac{1}{7}\). Oblicz, ile jest losów pustych.

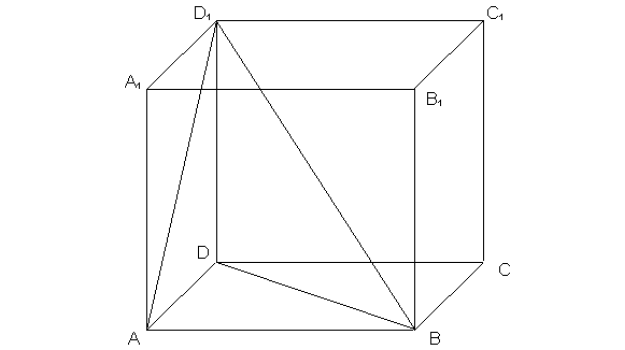
Podstawą prostopadłościanu \(ABCD{A_1}{B_1}{C_1}{D_1}\) jest prostokąt o bokach długości: \(\left| {\overline {AD} } \right| = 3\) i \(\left| {\overline {AB} } \right| = 6\,.\) Wysokość prostopadłościanu ma długość równą 6. Uzasadnij, za pomocą rachunków, że trójkąt \(BA{D_1}\) jest prostokątny.