Matura z matematyki 2013 – Maj podstawowy
Majowa matura z matematyki 2013 na poziomie podstawowym jest bardzo dobrym materiałem do zrozumienia najważniejszych działów matematycznych w liceum.
Arkusz i odpowiedzi Centralnej Komisji Edukacyjnej
- Matura z matematyki 2013 – Maj Poziom Podstawowy – Arkusz CKE
- Matura z matematyki 2013 – Maj Poziom Podstawowy – Odpowiedzi CKE
Poniżej przedstawiam wszystkie rozwiązane zadania maturalne w formie video, które są idealnym treningiem do zdania tegorocznej matury.
Matura z matematyki 2013 – Zadania i odpowiedzi online
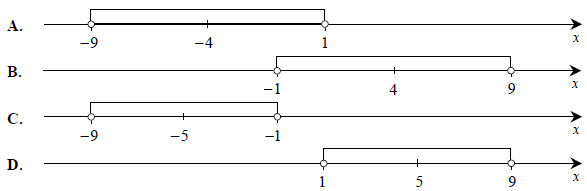
Wskaż rysunek, na którym zaznaczony jest zbiór wszystkich liczb rzeczywistych spełniających nierówność \( \left| {x + 4} \right| < 5 \) .
Liczby a i b są dodatnie oraz 12% liczby a jest równe 15% liczby b. Stąd wynika, że a jest równe
Liczba log100 – log28 jest równa
Rozwiązaniem układu równań \(\left\{ {\begin{array}{*{20}{c}}{5x + 3\,y = 3}\\{8x – 6y = 48}\end{array}} \right.\) jest para liczb
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Punkt A = (0,1) leży na wykresie funkcji liniowej f (x) = (m – 2)x + m – 3 . Stąd wynika, że
Wierzchołkiem paraboli o równaniu y = -3(x – 2)2 + 4 jest punkt o współrzędnych
Dla każdej liczby rzeczywistej x , wyrażenie 4x2 – 12x + 9 jest równe
Prosta o równaniu \( f(x) = \frac{2}{m}x + 1\) jest prostopadła do prostej o równaniu \(f(x) = – \frac{3}{2}x – 1\) . Stąd wynika, że
Na rysunku przedstawiony jest fragment wykresu pewnej funkcji liniowej y = ax + b .
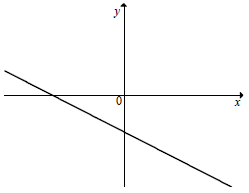
Jakie znaki mają współczynniki a i b ?
Najmniejszą liczbą całkowitą spełniającą nierówność \(\frac{x}{2} \le \frac{{2x}}{3} + \frac{1}{4}\) jest
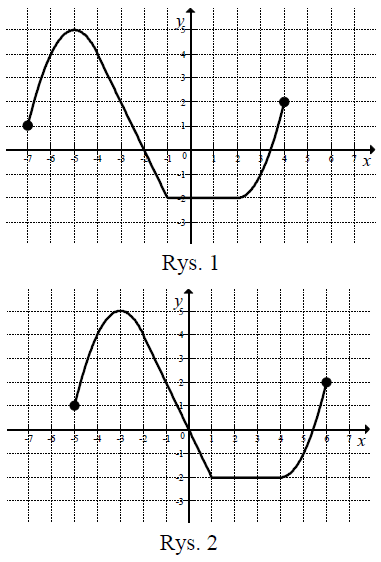
Na rysunku 1 przedstawiony jest wykres funkcji y = f (x) określonej dla x =< -7,4>.
Rysunek 2 przedstawia wykres funkcji
Ciąg (27, 18, x + 5) jest geometryczny. Wtedy
Ciąg (an) określony dla n ≥ 1 jest arytmetyczny oraz a3 = 10 i a4 = 14 . Pierwszy wyraz tego ciągu jest równy
Kąt \(\alpha\) jest ostry i \({\rm{sin }}\alpha = \frac{{\sqrt 3 }}{2}\) . Wartość wyrażenia \({\cos ^2}\alpha – 2\) jest równa
Średnice AB i CD okręgu o środku S przecinają się pod kątem 50° (tak jak na rysunku).
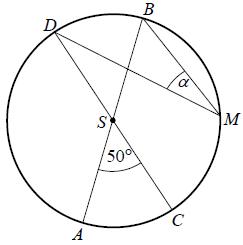
Miara kąta \(\alpha\) jest równa
Liczba rzeczywistych rozwiązań równania (x+1)(x+2)(x2+3)=0 jest równa
Punkty A = (-1,2) i B = (5,-2) są dwoma sąsiednimi wierzchołkami rombu ABCD. Obwód tego rombu jest równy
Punkt S=(-4, 7) jest środkiem odcinka PQ, gdzie Q=(17, 12). Zatem punkt P ma współrzędne
Odległość między środkami okręgów o równaniach (x+1)2 + (y-2)2 = 9 oraz x2 + y2 = 10 jest równa
Liczba wszystkich krawędzi graniastosłupa jest o 10 większa od liczby wszystkich jego ścian bocznych. Stąd wynika, że podstawą tego graniastosłupa jest
Pole powierzchni bocznej stożka o wysokości 4 i promieniu podstawy 3 jest równe
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Niech p oznacza prawdopodobieństwo zdarzenia, że iloczyn liczb wyrzuconych oczek jest równy 5. Wtedy
Liczba \(\frac{{\sqrt {50} – \sqrt {18} }}{{\sqrt 2 }}\) jest równa
Mediana uporządkowanego niemalejąco zestawu sześciu liczb: 1, 2, 3, x, 5, 8 jest równa 4. Wtedy
Objętość graniastosłupa prawidłowego trójkątnego o wysokości 7 jest równa \(28\sqrt 3 \). Długość krawędzi podstawy tego graniastosłupa jest równa
Rozwiąż równanie \({x^3} + 2{x^2} – 8x – 16 = 0\)
Treść dostępna po opłaceniu abonamentu.Kąt \(\alpha\) jest ostry i \(\sin \alpha = \frac{{\sqrt 3 }}{2}\) . Oblicz wartość wyrażenia \({\sin ^2}\alpha – 3{\cos ^2}\alpha \)
Treść dostępna po opłaceniu abonamentu.Udowodnij, że dla dowolnych liczb rzeczywistych x, y, z takich, że x+y+z=0, prawdziwa jest nierówność \(xy + yz + zx \le 0\). Możesz skorzystać z tożsamości \({(x + y + z)^2} = {x^2} + {y^2} + {z^2} + 2xy + 2xz + 2yz\).
Treść dostępna po opłaceniu abonamentu.Na rysunku przedstawiony jest wykres funkcji f(x) określonej dla x= < -7,8>.
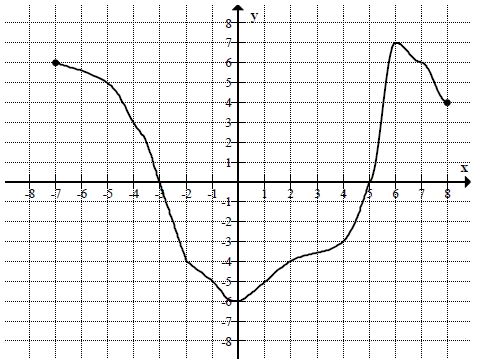
Odczytaj z wykresu i zapisz:
a) największą wartość funkcji f
b) zbiór rozwiązań nierówności f(x) < 0 .
Treść dostępna po opłaceniu abonamentu.Rozwiąż nierówność \(2{x^2} – 7x + 5 \ge 0\)
Treść dostępna po opłaceniu abonamentu.Wykaż, że liczba \({6^{100}} – 2 \cdot {6^{99}} + 10 \cdot {6^{98}}\) jest podzielna przez 17.
Treść dostępna po opłaceniu abonamentu.Punkt S jest środkiem okręgu opisanego na trójkącie ostrokątnym ABC. Kąt ACS jest trzy razy większy od kąta BAS, a kąt CBS jest dwa razy większy od kąta BAS. Oblicz kąty trójkąta ABC.
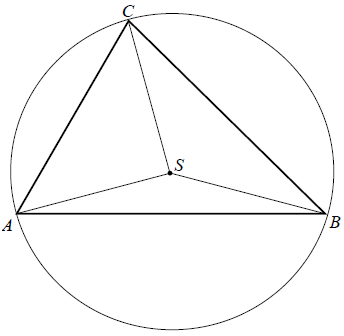 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Pole podstawy ostrosłupa prawidłowego czworokątnego jest równe 100 cm2, a jego pole powierzchni bocznej jest równe 260 cm2. Oblicz objętość tego ostrosłupa.
Treść dostępna po opłaceniu abonamentu.Dwa miasta łączy linia kolejowa o długości 336 kilometrów. Pierwszy pociąg przebył tę trasę w czasie o 40 minut krótszym niż drugi pociąg. Średnia prędkość pierwszego pociągu na tej trasie była o 9 km/h większa od średniej prędkości drugiego pociągu. Oblicz średnią prędkość każdego z tych pociągów na tej trasie.
Treść dostępna po opłaceniu abonamentu.- Matura z matematyki 2017 – Maj podstawowa
- Matura z matematyki 2016 – Maj podstawowa
- Matura z matematyki 2015 – Maj podstawowa
- Matura z matematyki 2014 – Maj podstawowa
- Matura z matematyki 2013 – Maj podstawowa
- Matura z matematyki 2012 – Maj podstawowa
- Matura z matematyki 2011 – Maj podstawowa
- Matura z matematyki 2010 – Maj podstawowa
- Matura z matematyki 2009 – Maj podstawowa
- Matura z matematyki 2008 – Maj podstawowa
- Matura z matematyki 2007 – Maj podstawowa
- Matura z matematyki 2006 – Maj podstawowa
- Matura z matematyki 2005 – Maj podstawowa
- Matura z matematyki 2003 – Maj podstawowa