Matura z matematyki 2007 – Maj podstawowa

Znajdź wzór funkcji kwadratowej y = f (x) , której wykresem jest parabola o wierzchołku (1,–9) przechodząca przez punkt o współrzędnych (2,–8). Otrzymaną funkcję przedstaw w postaci kanonicznej. Oblicz jej miejsca zerowe i naszkicuj wykres.

Wysokość prowizji, którą klient płaci w pewnym biurze maklerskim przy każdej zawieranej transakcji kupna lub sprzedaży akcji jest uzależniona od wartości transakcji. Zależność ta została przedstawiona w tabeli:

Klient zakupił za pośrednictwem tego biura maklerskiego 530 akcji w cenie 25 zł za jedną akcję. Po roku sprzedał wszystkie kupione akcje po 45 zł za jedną sztukę. Oblicz, ile zarobił na tych transakcjach po uwzględnieniu prowizji, które zapłacił.

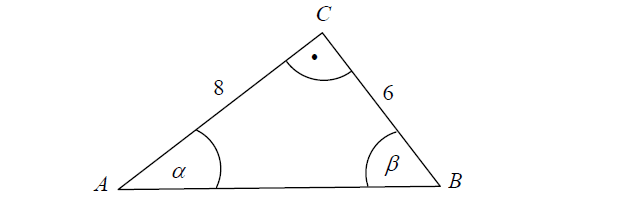
Korzystając z danych przedstawionych na rysunku, oblicz wartość wyrażenia: $$t{g^2}\beta – 5\sin \beta \cdot ctg\alpha + \sqrt {1 – {{\cos }^2}\alpha } .$$

Samochód przebył w pewnym czasie 210 km. Gdyby jechał ze średnią prędkością o 10 km/h większą, to czas przejazdu skróciłby się o pół godziny. Oblicz, z jaką średnią prędkością jechał ten samochód.

Dany jest ciąg arytmetyczny $\left( {{a_n}} \right)\,,$ gdzie $n \ge 1\,.$ Wiadomo, że dla każdego $n \ge 1\,$suma n początkowych wyrazów ${S_n} = {a_1} + {a_2} + \,…\, + {a_n}$ wyraża się wzorem: ${S_n} = – {n^2} + 13n\,.$
a) Wyznacz wzór na n–ty wyraz ciągu $\left( {{a_n}} \right)\,$.
b) Oblicz ${a_{2007}}$.
c) Wyznacz liczbę n, dla której ${a_n} = 0$.

Dany jest wielomian $W\left( x \right) = 2{x^3} + a{x^2} – 14x + b\,.$
a) Dla a = 0 i b = 0 otrzymamy wielomian $W\left( x \right) = 2{x^3} – 14x.$
Rozwiąż równanie $2{x^3} – 14x = 0$
b) Dobierz wartości a i b tak, aby wielomian W(x) był podzielny jednocześnie przez x − 2 oraz przez x + 3 .

Dany jest punkt C = (2,3) i prosta o równaniu y = 2x −8 będąca symetralną odcinka BC. Wyznacz współrzędne punktu B. Wykonaj obliczenia uzasadniające odpowiedź.

Na stole leżało 14 banknotów: 2 banknoty o nominale 100 zł, 2 banknoty o nominale 50 zł i 10 banknotów o nominale 20 zł. Wiatr zdmuchnął na podłogę 5 banknotów. Oblicz prawdopodobieństwo tego, że na podłodze leży dokładnie 130 zł. Odpowiedź podaj w postaci ułamka nieskracalnego.

Oblicz pole czworokąta wypukłego ABCD, w którym kąty wewnętrzne mają odpowiednio miary: $\sphericalangle A=90{}^\circ ,\ \sphericalangle B=75{}^\circ ,\ \sphericalangle C=60{}^\circ ,\ \sphericalangle D=135{}^\circ$, a boki AB i AD mają długość 3cm. Sporządź rysunek pomocniczy.

Dany jest graniastosłup czworokątny prosty ABCDEFGH o podstawach ABCD i EFGH oraz krawędziach bocznych AE, BF, CG, DH. Podstawa ABCD graniastosłupa jest rombem o boku długości 8 cm i kątach ostrych A i C o mierze $60^\circ .$ Przekątna graniastosłupa CE jest nachylona do płaszczyzny podstawy pod kątem $60^\circ .$ Sporządź rysunek pomocniczy i zaznacz na nim wymienione w zadaniu kąty. Oblicz objętość tego graniastosłupa.

Dany jest rosnący ciąg geometryczny $\left( {{a_n}} \right)$ dla $n \ge 1$, w którym ${a_1} = x,\quad {a_2} = 14,\quad {a_3} = y.$ Oblicz x oraz y, jeżeli wiadomo, że x + y = 35 .