Matura z matematyki 2009 – Maj podstawowa
Czy wiesz, że matura z matematyki 2009 jest idealnym materiałem ćwiczeniowym do kolejnych egzaminów maturalnych? Zobacz arkusz i odpowiedzi do zadań online.
Arkusz Centralnej Komisji Edukacyjnej
- Matura z matematyki 2009 – Maj Poziom Podstawowy – Arkusz
Zapamiętaj!
- Niektóre zadania maturalne co roku powtarzają się – zmieniają się tylko dane do zadania i liczby.
Matura z matematyki 2009 – zadania i odpowiedzi
Funkcja f określona jest wzorem \(f(x) = \left\{ {\begin{array}{*{20}{c}}{2x – 3\quad \,\,dla\;\quad x < 2\quad \;}\\{\;\;\quad 1\quad \quad dla\;\quad 2 \le x \le 4}\end{array}} \right.\)
a) Uzupełnij tabelę:

b) Narysuj wykres funkcji f .
c) Podaj wszystkie liczby całkowite x , spełniające nierówność \(f\left( x \right){\rm{ }} \ge {\rm{ }} – 6{\rm{ }}.\)
Dwaj rzemieślnicy przyjęli zlecenie wykonania wspólnie 980 detali. Zaplanowali, że każdego dnia pierwszy z nich wykona m, a drugi n detali. Obliczyli, że razem wykonają zlecenie w ciągu 7 dni. Po pierwszym dniu pracy pierwszy z rzemieślników rozchorował się i wtedy drugi, aby wykonać całe zlecenie, musiał pracować o 8 dni dłużej niż planował, (nie zmieniając liczby wykonywanych codziennie detali). Oblicz m i n .
Wykres funkcji f danej wzorem f (x) = -2x2 przesunięto wzdłuż osi Ox o 3 jednostki w prawo oraz wzdłuż osi Oy o 8 jednostek w górę, otrzymując wykres funkcji g .
a) Rozwiąż nierówność f (x) + 5 < 3x .
b) Podaj zbiór wartości funkcji g .
c) Funkcja g określona jest wzorem \(g\left( x \right) = – 2{x^2} + bx + c.\) Oblicz b i c.
Odpowiedź do punktu a)Wykaż, że liczba \({3^{54}}\) jest rozwiązaniem równania \({243^{11}} – {81^{14}} + 7x = {9^{27}}.\)
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Wielomian W dany jest wzorem \(W(x) = {x^3} + a{x^2} – 4x + b.\)
a) Wyznacz a, b oraz c tak, aby wielomian W był równy wielomianowi P, gdy \[P(x) = {x^3} + \left( {2a + 3} \right){x^2} + \left( {a + b + c} \right)x – 1.\]
b) Dla a = 3 i b = 0 zapisz wielomian W w postaci iloczynu trzech wielomianów stopnia pierwszego.
Odpowiedź do punktu a)
Treść dostępna po opłaceniu abonamentu.Odpowiedź do punktu b)
Treść dostępna po opłaceniu abonamentu.Miara jednego z kątów ostrych w trójkącie prostokątnym jest równa \(\alpha .\)
a) Uzasadnij, że spełniona jest nierówność \(\sin \alpha – tg\alpha < 0.\)
b) Dla \(\sin \alpha = \frac{{2\sqrt 2 }}{3}\) oblicz wartość wyrażenia \({\cos ^3}\alpha + \cos \alpha \cdot {\sin ^2}\alpha .\)
Odpowiedź do punktu a)
Treść dostępna po opłaceniu abonamentu.Odpowiedź do punktu b)
Treść dostępna po opłaceniu abonamentu.Dany jest ciąg arytmetyczny \(\left( {{a}_{n}} \right)\) dla \(n \ge 1\) w którym \({a_7} = 1,\quad {a_{11}} = 9.\)
a) Oblicz pierwszy wyraz \({a_1}\) i różnicę r ciągu \(\left( {{a}_{n}} \right)\).
b) Sprawdź, czy ciąg \(\left( {{a_7},{a_8},{a_{11}}} \right)\)jest geometryczny.
c) Wyznacz takie n, aby suma n początkowych wyrazów ciągu \(\left( {{a}_{n}} \right)\) miała wartość najmniejszą.
Odpowiedź do punktu a) Treść dostępna po opłaceniu abonamentu.Odpowiedź do punktu b)
Treść dostępna po opłaceniu abonamentu.Odpowiedź do punktu c)
Treść dostępna po opłaceniu abonamentu.W trapezie ABCD długość podstawy CD jest równa 18 , a długości ramion trapezu AD i BC są odpowiednio równe 25 i 15. Kąty ADB i DCB, zaznaczone na rysunku, mają równe miary. Oblicz obwód tego trapezu.
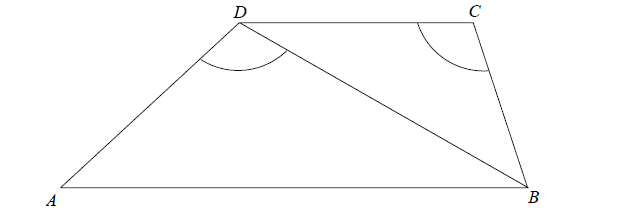 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Punkty B = (0,10) i O = (0,0) są wierzchołkami trójkąta prostokątnego OAB, w którym \( \left| \sphericalangle OAB \right|=90{}^\circ \). Przyprostokątna OA zawiera się w prostej o równaniu \(y = \frac{1}{2}x\,.\) Oblicz współrzędne punktu A i długość przyprostokątnej OA.
Treść dostępna po opłaceniu abonamentu.Tabela przedstawia wyniki części teoretycznej egzaminu na prawo jazdy. Zdający uzyskał wynik pozytywny, jeżeli popełnił co najwyżej dwa błędy.
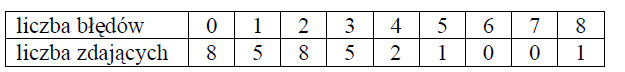
a) Oblicz średnią arytmetyczną liczby błędów popełnionych przez zdających ten egzamin. Wynik podaj w zaokrągleniu do całości.
b) Oblicz prawdopodobieństwo, że wśród dwóch losowo wybranych zdających tylko jeden uzyskał wynik pozytywny. Wynik zapisz w postaci ułamka zwykłego nieskracalnego.
Treść dostępna po opłaceniu abonamentu.Powierzchnia boczna walca po rozwinięciu na płaszczyznę jest prostokątem. Przekątna tego prostokąta ma długość 12 i tworzy z bokiem, którego długość jest równa wysokości walca, kąt o mierze \(30^\circ .\)
a) Oblicz pole powierzchni bocznej tego walca.
b) Sprawdź, czy objętość tego walca jest większa od \(18\sqrt 3 \). Odpowiedź uzasadnij.
Treść dostępna po opłaceniu abonamentu.- Matura z matematyki 2017 – Maj podstawowa
- Matura z matematyki 2016 – Maj podstawowa
- Matura z matematyki 2015 – Maj podstawowa
- Matura z matematyki 2014 – Maj podstawowa
- Matura z matematyki 2013 – Maj podstawowa
- Matura z matematyki 2012 – Maj podstawowa
- Matura z matematyki 2011 – Maj podstawowa
- Matura z matematyki 2010 – Maj podstawowa
- Matura z matematyki 2009 – Maj podstawowa
- Matura z matematyki 2008 – Maj podstawowa
- Matura z matematyki 2007 – Maj podstawowa
- Matura z matematyki 2006 – Maj podstawowa
- Matura z matematyki 2005 – Maj podstawowa
- Matura z matematyki 2003 – Maj podstawowa




