Próbna matura z matematyki 2015 CKE

Liczba 0,6 jest jednym z przybliżeń liczby \(\frac{5}{8}\). Błąd względny tego przybliżenia, wyrażony w procentach, jest równy

Dany jest okrąg o środku S=(-6,-8) i promieniu 2014. Obrazem tego okręgu w symetrii osiowej względem osi Oy jest okrąg o środku w punkcie S₁. Odległość między punktami S i S₁ jest równa

Rozwiązaniami równania (x³-8)(x-5)(2x+1)=0 są liczby

Cena towaru została podwyższona o 30%, a po pewnym czasie nową, wyższą cenę ponownie podwyższono, tym razem o 10%. W rezultacie obu podwyżek wyjściowa cena towaru zwiększyła się o

Dane są dwie funkcje określone dla wszystkich liczb rzeczywistych x wzorami f(x)=-5x+1 oraz g(x)=5^x. Liczba punktów wspólnych wykresów tych funkcji jest równa

Wyrażenie (3x+1+y)² jest równe

Połowa sumy 4²⁸+4²⁸+4²⁸+4²⁸ jest równa

Równania \(y=-\frac{3}{4}x+\frac{5}{4}\quad oraz\quad y=-\frac{4}{3}\) opisują dwie proste

Na płaszczyźnie dane są punkty: \(A=\left( \sqrt{2},\sqrt{6} \right),\ B=\left( 0,0 \right)\ i\ C=\left( \sqrt{2},0 \right)\). Kąt BAC jest równy

Funkcja f, określona dla wszystkich liczb całkowitych dodatnich, przyporządkowuje liczbie x ostatnią cyfrę jej kwadratu. Zbiór wartości funkcji f zawiera dokładnie

Ekipa złożona z 25 pracowników wymieniła tory kolejowe na pewnym odcinku w ciągu 156 dni. Jeśli wymianę torów kolejowych na kolejnym odcinku o tej samej długości trzeba przeprowadzić w ciągu 100 dni, to, przy założeniu takiej samej wydajności, należy zatrudnić do pracy o

Z sześcianu ABCDEFGH o krawędzi długości a odcięto ostrosłup ABDE (zobacz rysunek).

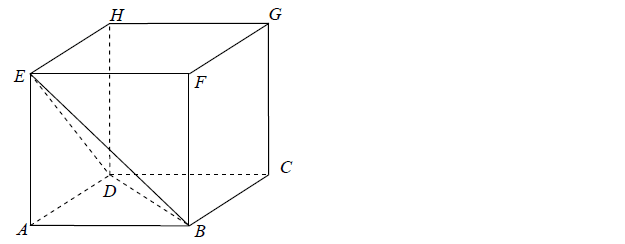
Ile razy objętość tego ostrosłupa jest mniejsza od objętości pozostałej części sześcianu?

W układzie współrzędnych narysowano część paraboli o wierzchołku w punkcie A=(2,4), która jest wykresem funkcji kwadratowej f.

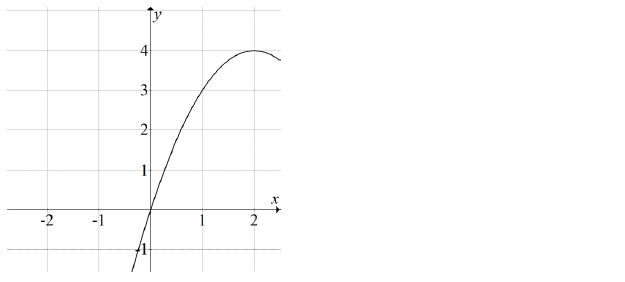
Funkcja f może być opisana wzorem

Punkty \(A=\left( -6-2\sqrt{2},4-2\sqrt{2} \right),\ B=\left( 2+4\sqrt{2},-6\sqrt{2} \right),\ C=\left( 2+6\sqrt{2},6-2\sqrt{2} \right)\) są kolejnymi wierzchołkami równoległoboku ABCD. Przekątne tego równoległoboku przecinają się w punkcie

Liczba sin150° jest równa liczbie

Na ścianie kamienicy zaprojektowano mural utworzony z szeregu trójkątów równobocznych różnej wielkości. Najmniejszy trójkąt ma bok długości 1 m, a bok każdego z następnych trójkątów jest o 10 cm dłuższy niż bok poprzedzającego go trójkąta. Ostatni trójkąt ma bok długości 5,9 m. Ile trójkątów przedstawia mural?

Dany jest trójkąt równoramienny, w którym ramię o długości 20 tworzy z podstawą kąt 67,5°.Pole tego trójkąta jest równe

Na rysunkach poniżej przedstawiono siatki dwóch ostrosłupów.

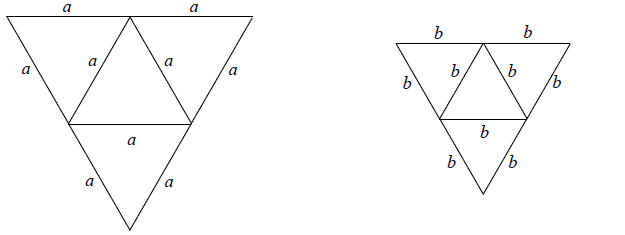
Pole powierzchni całkowitej ostrosłupa o krawędzi a jest dwa razy większe od pola powierzchni całkowitej ostrosłupa o krawędzi b. Ile razy objętość ostrosłupa o krawędzi a jest większa od objętości ostrosłupa o krawędzi b?

Na okręgu o środku S leżą punkty A, B, C i D. Odcinek AB jest średnicą tego okręgu. Kąt między tą średnicą a cięciwą AC jest równy 21° (zobacz rysunek).

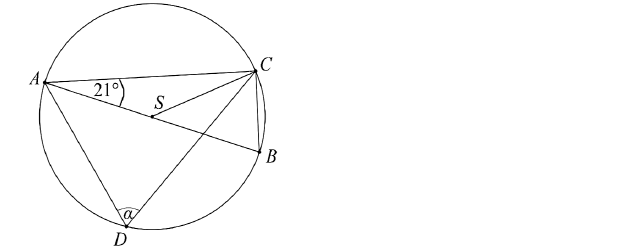
Kąt \(\alpha \) między cięciwami AD i CD jest równy

Średnia arytmetyczna zestawu danych: 3, 8, 3, 11, 3, 10, 3, x jest równa 6. Mediana tego zestawu jest równa

Dany jest ciąg geometryczny (a_n), w którym \({{a}_{1}}=-\sqrt{2},\ {{a}_{2}}=2,\ {{a}_{3}}=-2\sqrt{2}\). Dziesiąty wyraz tego ciągu, czyli a₁₀ jest równy

Ciąg (a_n) jest określony wzorem \({{a}_{n}}=\frac{24-4n}{n}\quad dla\quad n\ge 1\). Liczba wszystkich całkowitych nieujemnych wyrazów tego ciągu jest równa

Rzucamy sześć razy symetryczną sześcienną kostką do gry. Niech p_i oznacza prawdopodobieństwo wyrzucenia i oczek w i-tym rzucie. Wtedy

Wskaż liczbę, która spełnia równanie 4^x=9.

Rozwiąż nierówność: -x²-4x+21<0

Uzasadnij, że żadna liczba całkowita nie jest rozwiązaniem równania \(\frac{2x+4}{x-2}=2x+1\).

Czas połowicznego rozpadu pierwiastka to okres, jaki jest potrzebny, by ze 100% pierwiastka pozostało 50% tego pierwiastka. Oznacza to, że ilość pierwiastka pozostała z każdego grama pierwiastka po x okresach rozpadu połowicznego wyraża się wzorem \(y={{\left( \frac{1}{2} \right)}^{x}}\). W przypadku izotopu jodu ¹³¹I czas połowicznego rozpadu jest równy 8 dni. Wyznacz najmniejszą liczbę dni, po upływie których pozostanie z 1 g ¹³¹I nie więcej niż 0,125 g tego pierwiastka.

Uzasadnij, że jeżeli liczba całkowita nie dzieli się przez 3, to jej kwadrat przy dzieleniu przez 3 daje resztę 1.

Wartość prędkości średniej obliczamy jako iloraz drogi i czasu, w którym ta droga została przebyta. Samochód przejechał z miejscowości A do miejscowości C przez miejscowość B, która znajduje się w połowie drogi z A do C. Wartość prędkości średniej samochodu na trasie z A do B była równa 40 km/h, a na trasie z B do C – 60km/h. Oblicz wartość prędkości średniej samochodu na całej trasie z A do C.

Zakupiono 16 biletów do teatru, w tym 10 biletów na miejsca od 1. do 10. w pierwszym rzędzie i 6 biletów na miejsca od 11. do 16. w szesnastym rzędzie. Jakie jest prawdopodobieństwo zdarzenia polegającego na tym, że 2 wylosowane bilety, spośród szesnastu, będą biletami na sąsiadujące miejsca?

W trapezie ABCD (AB||CD) przekątne AC i BD przecinają się w punkcie O takim, że |AO|:|OC|=5:1. Pole trójkąta AOD jest równe 10. Uzasadnij, że pole trapezu ABCD jest równe 72.

Punkty A=(3,3) i B=(9,1) są wierzchołkami trójkąta ABC, a punkt M=(1,6) jest środkiem boku AC. Oblicz współrzędne punktu przecięcia prostej AB z wysokością tego trójkąta, poprowadzoną z wierzchołka C.

Tworząca stożka ma długość 17, a wysokość stożka jest krótsza od średnicy jego podstawy o 22. Oblicz pole powierzchni całkowitej i objętość tego stożka.