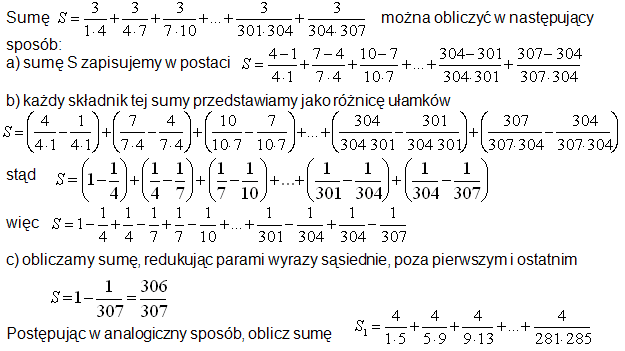Matura z matematyki 2006 – Maj podstawowa
Zobacz już teraz maturę z matematyki 2006 online. Oceń poziom trudności zadań maturalnych. Skorzystaj z filmowych odpowiedzi w przypadku trudności w rozwiązaniu zadania.
Arkusz i odpowiedzi – Centralna Komisja Edukacyjna
- Matura z matematyki 2006 – Maj Poziom Podstawowy – Arkusz CKE
- Matura z matematyki 2006 – Maj Poziom Podstawowy – Odpowiedzi CKE
Zadania maturalne online – odpowiedzi wideo
Dane są zbiory: \(A = \left\{ {\,x \in R:\left| {x – 4} \right| \ge 7} \right\}\,,\;B = \left\{ {\,x \in R:{x^2} > 0} \right\}\,.\) Zaznacz na osi liczbowej:
a) zbiór A,
b) zbiór B,
c) zbiór C = B \ A.
W wycieczce szkolnej bierze udział 16 uczniów, wśród których tylko czworo zna okolicę. Wychowawca chce wybrać w sposób losowy 3 osoby, które mają pójść do sklepu. Oblicz prawdopodobieństwo tego, że wśród wybranych trzech osób będą dokładnie dwie znające okolicę.
Kostka masła produkowanego przez pewien zakład mleczarski ma nominalną masę 20 dag. W czasie kontroli zakładu zważono 150 losowo wybranych kostek masła. Wyniki badań przedstawiono w tabeli.
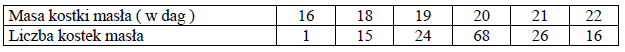
a) Na podstawie danych przedstawionych w tabeli oblicz średnią arytmetyczną oraz odchylenie standardowe masy kostki masła.
b) Kontrola wypada pozytywnie, jeśli średnia masa kostki masła jest równa masie nominalnej i odchylenie standardowe nie przekracza 1 dag. Czy kontrola zakładu wypadła pozytywnie? Odpowiedź uzasadnij.
Dany jest rosnący ciąg geometryczny, w którym \({a_1} = 12,\;{a_3} = 27\,.\)
a) Wyznacz iloraz tego ciągu.
b) Zapisz wzór, na podstawie którego można obliczyć wyraz \({a_n},\) dla każdej liczby naturalnej
\(n \ge 1\,.\)
c) Oblicz wyraz \({a_6}.\)
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Wiedząc, że \({0^\circ} \le \alpha \le 360^\circ ,\;\,\sin \alpha < 0\;\,oraz\;4tg\alpha = 3{\sin ^2}\alpha + 3{\cos ^2}\alpha \)
a) oblicz tg α ,
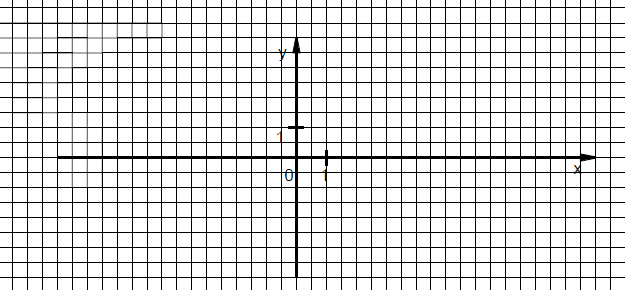
b) zaznacz w układzie współrzędnych kąt α i podaj współrzędne dowolnego punktu,
różnego od początku układu współrzędnych, który leży na końcowym ramieniu tego
kąta.
 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
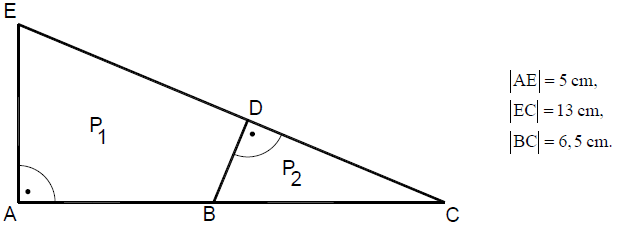
Państwo Nowakowie przeznaczyli 26000 zł na zakup działki. Do jednej z ofert dołączono rysunek dwóch przylegających do siebie działek w skali 1:1000. Jeden metr kwadratowy gruntu w tej ofercie kosztuje 35 zł. Oblicz, czy przeznaczona przez państwa Nowaków kwota wystarczy na zakup działki \({P_2}\,.\)
 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Szkic przedstawia kanał ciepłowniczy, którego przekrój poprzeczny jest prostokątem. Wewnątrz kanału znajduje się rurociąg składający się z trzech rur, każda o średnicy zewnętrznej 1 m. Oblicz wysokość i szerokość kanału ciepłowniczego. Wysokość zaokrąglij do 0,01 m.
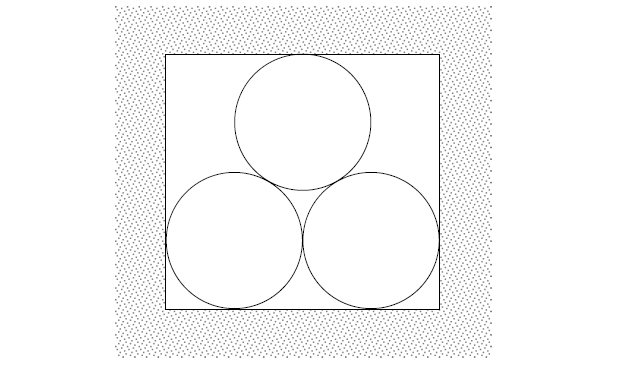 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Dana jest funkcja \(f\left( x \right) = – {x^2} + 6x – 5.\)
a) Naszkicuj wykres funkcji f i podaj jej zbiór wartości.
b) Podaj rozwiązanie nierówności \(f\left( x \right) \ge 0\,.\)
 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Dach wieży ma kształt powierzchni bocznej ostrosłupa prawidłowego czworokątnego,
którego krawędź podstawy ma długość 4 m. Ściana boczna tego ostrosłupa jest nachylona do
płaszczyzny podstawy pod kątem \(60^\circ .\)
a) Sporządź pomocniczy rysunek i zaznacz na nim podane w zadaniu wielkości.
b) Oblicz, ile sztuk dachówek należy kupić, aby pokryć ten dach, wiedząc, że do pokrycia
\(1{m^2}\) potrzebne są 24 dachówki. Przy zakupie należy doliczyć 8% dachówek na zapas.
Liczby 3 i –1 są pierwiastkami wielomianu \(W\left( x \right) = 2{x^3} + a{x^2} + bx + 30.\)
a) Wyznacz wartości współczynników a i b.
b) Oblicz trzeci pierwiastek tego wielomianu.
- Matura z matematyki 2017 – Maj podstawowa
- Matura z matematyki 2016 – Maj podstawowa
- Matura z matematyki 2015 – Maj podstawowa
- Matura z matematyki 2014 – Maj podstawowa
- Matura z matematyki 2013 – Maj podstawowa
- Matura z matematyki 2012 – Maj podstawowa
- Matura z matematyki 2011 – Maj podstawowa
- Matura z matematyki 2010 – Maj podstawowa
- Matura z matematyki 2009 – Maj podstawowa
- Matura z matematyki 2008 – Maj podstawowa
- Matura z matematyki 2007 – Maj podstawowa
- Matura z matematyki 2006 – Maj podstawowa
- Matura z matematyki 2005 – Maj podstawowa
- Matura z matematyki 2003 – Maj podstawowa