Matura z matematyki 2005 – Maj podstawowa
Majowa matura z matematyki 2005 przeszła już do historii. Zobacz arkusz i odpowiedzi – oceń skalę trudności zadań. Sprawdź, czy poradziłbyś sobie z arkuszem Centralnej Komisji Edukacyjnej?
Arkusz i odpowiedzi Centralnej Komisji Edukacyjnej
- Matura z matematyki 2005 – Maj Poziom Podstawowy – Arkusz CKE
- Matura z matematyki 2005 – Maj Poziom Podstawowy – Odpowiedzi CKE
Zadania maturalne z matematyki 2005 – odpowiedzi
W pudełku są trzy kule białe i pięć kul czarnych. Do pudełka można albo dołożyć jedną kulę białą albo usunąć z niego jedną kulę czarną, a następnie wylosować z tego pudełka jedną kulę. W którym z tych przypadków wylosowanie kuli białej jest bardziej prawdopodobne? Wykonaj odpowiednie obliczenia.
Dany jest ciąg \(\left( {{a_n}} \right)\,,\) gdzie \({a_n} = \frac{{n + 2}}{{3n + 1}}\quad dla\quad n = 1,2,3…\) Wyznacz wszystkie wyrazy tego ciągu większe od \(\frac{1}{2}.\)
Dany jest wielomian \(W\left( x \right) = {x^3} + k{x^2} – 4.\)
a) Wyznacz współczynnik k tego wielomianu wiedząc, że wielomian ten jest podzielny przez dwumian x + 2.
b) Dla wyznaczonej wartości k rozłóż wielomian na czynniki i podaj wszystkie jego pierwiastki.
Na trzech półkach ustawiono 76 płyt kompaktowych. Okazało się, że liczby płyt na półkach górnej, środkowej i dolnej tworzą rosnący ciąg geometryczny. Na środkowej półce stoją 24 płyty. Oblicz, ile płyt stoi na półce górnej, a ile płyt stoi na półce dolnej.
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Sklep sprowadza z hurtowni kurtki płacąc po 100 zł za sztukę i sprzedaje średnio 40 sztuk miesięcznie po 160 zł. Zaobserwowano, że każda kolejna obniżka ceny sprzedaży kurtki o 1 zł zwiększa sprzedaż miesięczną o 1 sztukę. Jaką cenę kurtki powinien ustalić sprzedawca, aby jego miesięczny zysk był największy?
Treść dostępna po opłaceniu abonamentu.Dane są zbiory liczb rzeczywistych: \[A = \left\{ {\;x:\left| {x + 2} \right|\left\langle 3 \right.} \right\}\] \[B = \left\{ {\;x:{{\left( {2x – 1} \right)}^3} \le 8{x^3} – 13{x^2} + 6x + 3} \right\}\] Zapisz w postaci przedziałów liczbowych zbiory A, B, A ∩ B oraz B − A.
Treść dostępna po opłaceniu abonamentu.W poniższej tabeli przedstawiono wyniki sondażu przeprowadzonego w grupie uczniów, dotyczącego czasu przeznaczanego dziennie na przygotowanie zadań domowych.
 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Z kawałka materiału o kształcie i wymiarach czworokąta ABCD (patrz na rysunek poniżej) wycięto okrągłą serwetkę o promieniu 3 dm. Oblicz, ile procent całego materiału stanowi jego niewykorzystana część. Wynik podaj z dokładnością do 0,01 procenta.
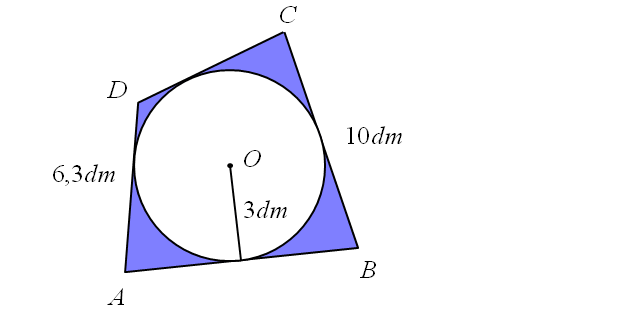 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Rodzeństwo w wieku 8 i 10 lat otrzymało razem w spadku 84100 zł. Kwotę tę złożono w banku, który stosuje kapitalizację roczną przy rocznej stopie procentowej 5%. Każde z dzieci otrzyma swoją część spadku z chwilą osiągnięcia wieku 21 lat. Życzeniem spadkodawcy było takie podzielenie kwoty spadku, aby w przyszłości obie wypłacone części spadku zaokrąglone do 1 zł były równe. Jak należy podzielić kwotę 84100 zł między rodzeństwo? Zapisz wszystkie wykonywane obliczenia.
Treść dostępna po opłaceniu abonamentu.W ostrosłupie czworokątnym prawidłowym wysokości przeciwległych ścian bocznych poprowadzone z wierzchołka ostrosłupa mają długości h i tworzą kąt o mierze 2α. Oblicz objętość tego ostrosłupa.
Treść dostępna po opłaceniu abonamentu.- Matura z matematyki 2017 – Maj podstawowa
- Matura z matematyki 2016 – Maj podstawowa
- Matura z matematyki 2015 – Maj podstawowa
- Matura z matematyki 2014 – Maj podstawowa
- Matura z matematyki 2013 – Maj podstawowa
- Matura z matematyki 2012 – Maj podstawowa
- Matura z matematyki 2011 – Maj podstawowa
- Matura z matematyki 2010 – Maj podstawowa
- Matura z matematyki 2009 – Maj podstawowa
- Matura z matematyki 2008 – Maj podstawowa
- Matura z matematyki 2007 – Maj podstawowa
- Matura z matematyki 2006 – Maj podstawowa
- Matura z matematyki 2005 – Maj podstawowa
- Matura z matematyki 2003 – Maj podstawowa




