Walec – zadania
Zobacz najważniejsze zadania i wzory pokazujące krok po kroku – jak obliczyć objętość walca i pole całkowite? Nie przegap głównych zadań, które mogą pojawić się w gimnazjum i liceum na sprawdzianie.
Objętość walca i pole całkowite – wzory i rozwiązania zadań
Ile zużyto blachy na wykonanie puszki o wymiarach podanych na rysunku.
Mając promień o długości 4 cm i wysokość H = 8 cm – oblicz objętość i pole całkowite walca.
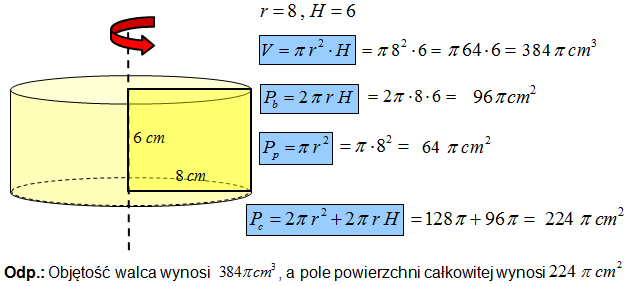
Oblicz objętość i pole całkowite walca powstałego w wyniku obrotu prostokąta o wymiarach 6 cm x 8 cm wokół krótszego boku.
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
W tym zadaniu wyobrażasz sobie, że wiertło wiertarki przechodzi przez krótszy bok prostokąta. Gdy włączysz wiertarkę wówczas prostokąt zacznie wirować i utworzy model walca o promieniu 8 cm i wysokości 6 cm. Dalej to zastosowanie wzorów na objętość i pole walca.
Przekątna przekroju osiowego walca (prostokąta) ma długość \(2\sqrt{41}\), a średnica podstawy ma długość 8. Oblicz objętość i pole całkowite tego walca.
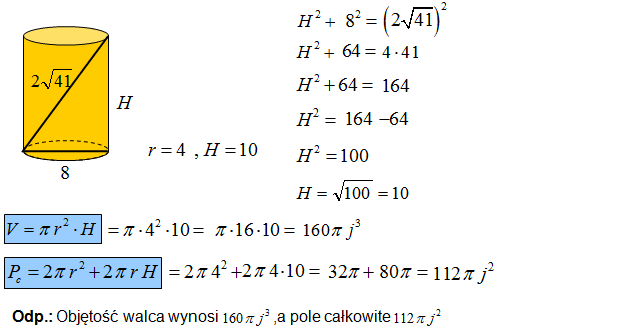Treść dostępna po opłaceniu abonamentu.
Jedyną trudnością jest obliczenie wysokości walca z Twierdzenia Pitagorasa.
Oblicz objętość i pole całkowite bryły powstałej w wyniku obrotu poniższej figury wokół narysowanej osi.
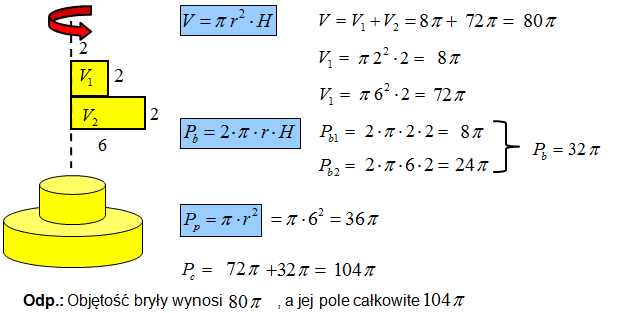Treść dostępna po opłaceniu abonamentu.
Oś obrotu zwykle zaznacz się przerywaną linią. Wyobrażasz sobie, że przez tę przerywaną linię przechodzi wiertło wiertarki. Podczas obrotu dana figura wiruje i tworzy nam bryłę podobną do walca. Konkretnie jest to bryła przypominająca dwa sklejone walce.
Objętość powstałej bryły to objętość dwóch sklejonych walców.
Obliczając pole całkowite należy obliczyć pole boczne mniejszego i większego walca. Dalej możesz obliczyć pole podstawy, czyli pole koła znajdującego się na dole bryły. Patrząc od góry na bryłę „z lotu ptaka” zauważysz pierścień i małe kółko wewnątrz tego pierścienia. Razem te dwie figury mają pole równe polu koła z podstawy bryły.
Jaką objętość wyznacza obracająca się trzepaczka do białka w kształcie prostokąta o wymiarach: 7 cm x 4 cm. O ile wzrośnie wyznaczana objętość, jeśli bok prostokąta o długości 4 cm zwiększymy 2 razy.
Treść dostępna po opłaceniu abonamentu.Przekrojem osiowym walca jest kwadrat o przekątnej \(8\sqrt{2}\). Oblicz objętość tego walca.
Treść dostępna po opłaceniu abonamentu.W sześcian o krawędzi 4 wpisano walec. Oblicz pole powierzchni bocznej tego walca.
Treść dostępna po opłaceniu abonamentu.W sześcian o przekątnej \(8\sqrt{3}\) wpisano walec. Oblicz pole boczne walca.
Treść dostępna po opłaceniu abonamentu.Prostokąt o boku 10 i przekątnej \(2\sqrt{26}\) obracamy wokół osi przechodzącej przez środki krótszych boków. Oblicz pole całkowite powstałego walca.
Treść dostępna po opłaceniu abonamentu.
O ile zwiększy się objętość walca jeżeli:
a) wysokość zwiększymy 3 razy, a promień pozostawimy bez zmiany
b) promień podstawy zwiększymy 2 razy, a wysokość pozostanie bez zmiany.
Oblicz wysokość walca o objętości \(16\pi c{{m}^{3}}\) i promieniu podstawy 2 cm.
Treść dostępna po opłaceniu abonamentu.Oblicz promień walca o wysokości 4 cm i objętości \(240\pi c{{m}^{3}}\)
Treść dostępna po opłaceniu abonamentu.Pole boczne walca wynosi \(80\pi c{{m}^{2}}\). Oblicz jego objętość jeśli jego wysokość wynosi 5 cm.
Treść dostępna po opłaceniu abonamentu.O ile zwiększy się poziom wody w beczce w kształcie walca o promieniu r = 8 cm jeżeli włożymy do niej dwie puszki w kształcie walca o promieniu 1 cm i wysokości 1 cm.
Treść dostępna po opłaceniu abonamentu.Oblicz objętość i pole całkowite walca , którego przekątna przekroju osiowego o długości \(8\sqrt{2}\) jest nachylona do podstawy pod kątem 45 °.
Treść dostępna po opłaceniu abonamentu.Oblicz objętość walca, którego przekrój jest prostokątem, którego przekątna o długości 6 jest nachylona do płaszczyzny podstawy pod kątem 30 °.
Treść dostępna po opłaceniu abonamentu.