Stożek
Definicja stożka:
„Stożek to bryła przestrzenna powstała przez obrót trójkąta prostokątnego wokół jednej z przyprostokątnych.”
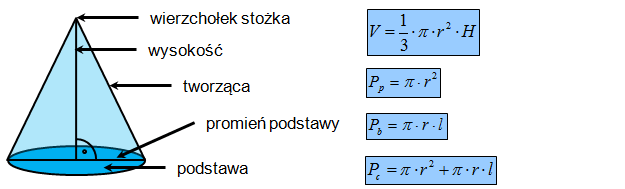
Wzór na objętość stożka:
\[\begin{align}
& V=\frac{1}{3}\cdot {{P}_{p}}\cdot H \\
& V=\frac{1}{3}\cdot \pi \cdot {{r}^{2}}\cdot H \\
\end{align}\]
Wzór na pole podstawy stożka:
\[{{P}_{p}}=\pi \cdot {{r}^{2}}\]
Wzór na pole boczne stożka:
\[{{P}_{b}}=\pi \cdot r\cdot l\]
Wzór na pole boczne stożka można łatwo zapamiętać przez skrót: „PRL–Polska Rzeczpospolita Ludowa”. P to inaczej \(\pi\), R to promień, L to tworząca.
Wzór na pole powierzchni całkowitej stożka:
\[\begin{align}
& {{P}_{c}}={{P}_{p}}+{{P}_{b}} \\
& {{P}_{c}}=\pi \cdot {{r}^{2}}+\pi \cdot r\cdot l \\
\end{align}\]
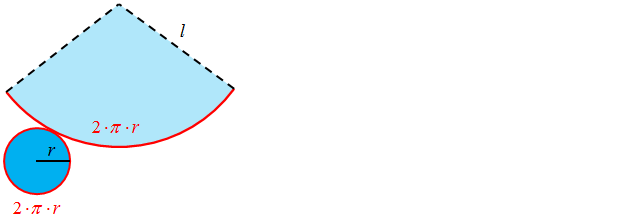
Warto zauważyć, że długość obwodu podstawy jest równa długości łuku będącego w polu bocznym. To są te zaznaczone na czerwono krzywe. Widzisz, że łączą się one podczas sklejania stożka.




