Matura z matematyki 2008 – Maj podstawowa
Matura z matematyki 2008 okazała się prosta. Zadania maturalne już teraz online! Sprawdź jaki był klucz odpowiedzi? Nie zwlekaj i dokonaj analizy zadań poniższego arkusza.
Arkusz i odpowiedzi Centralnej Komisji Edukacyjnej
- Matura z matematyki 2008 – Maj Poziom Podstawowy – Arkusz CKE
- Matura z matematyki 2008 – Maj Poziom Podstawowy – Odpowiedzi CKE
Musisz wiedzieć, że poniższe zadania maturalne są bardzo dobrym materiałem ćwiczeniowym dla tegorocznych maturzystów! Zauważ zależności pomiędzy maturami z poprzednich lat. Zwróć szczególną uwagę na te zadania maturalne, które co roku powtarzają się. Wtedy będziesz mógł skupić całą swoją uwagę na naukę tych konkretnych zagadnień. W efekcie zaoszczędzisz czas na inne sprawy, nie związane ze szkołą i nauką.
Matura z matematyki 2008 – zadania i odpowiedzi online
Na poniższym rysunku przedstawiono łamaną ABCD, która jest wykresem funkcji y = f ( x) .
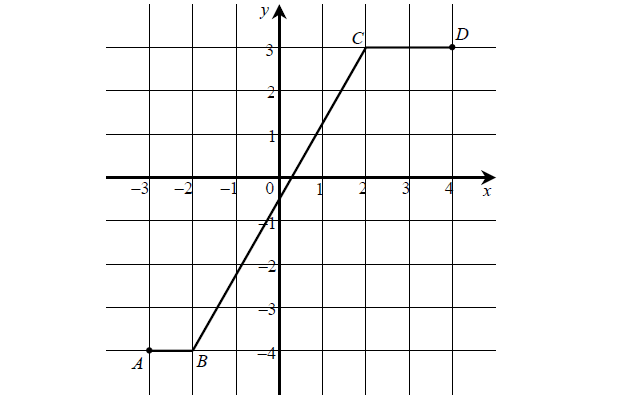
Korzystając z tego wykresu:
a) zapisz w postaci przedziału zbiór wartości funkcji f ,
b) podaj wartość funkcji f dla argumentu \(x = 1 – \sqrt {10} ,\)
c) wyznacz równanie prostej BC ,
d) oblicz długość odcinka BC .
Liczba przekątnych wielokąta wypukłego, w którym jest n boków i \(n \ge 3\)
wyraża się wzorem \(P\left( n \right) = \frac{{n\left( {n – 3} \right)}}{2}\)
Wykorzystując ten wzór:
a) oblicz liczbę przekątnych w dwudziestokącie wypukłym.
b) oblicz, ile boków ma wielokąt wypukły, w którym liczba przekątnych jest pięć razy
większa od liczby boków.
c) sprawdź, czy jest prawdziwe następujące stwierdzenie:
Każdy wielokąt wypukły o parzystej liczbie boków ma parzystą liczbę przekątnych.
Odpowiedź uzasadnij.
Rozwiąż równanie \({4^{23}}x – {32^9}x = {16^4} \cdot {\left( {{4^4}} \right)^4}\). Zapisz rozwiązanie tego równania w postaci \({2^k}\), gdzie k jest liczbą całkowitą.
Koncern paliwowy podnosił dwukrotnie w jednym tygodniu cenę benzyny, pierwszy raz o 10%, a drugi raz o 5%. Po obu tych podwyżkach jeden litr benzyny, wyprodukowanej przez ten koncern, kosztuje 4,62 zł. Oblicz cenę jednego litra benzyny przed omawianymi podwyżkami.
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Nieskończony ciąg liczbowy \(\left( {{a_n}} \right)\) jest określony wzorem \({a_n} = 2 – \frac{1}{n},\quad n = 1,2,3…\quad .\)
a) Oblicz, ile wyrazów ciągu \(\left( {{a_n}} \right)\) jest mniejszych od 1,975.
b) Dla pewnej liczby x trzywyrazowy ciąg \(\left( {{a_2},{a_7},x} \right)\) jest arytmetyczny. Oblicz x.
Prosta o równaniu 5x + 4y −10 = 0 przecina oś Ox układu współrzędnych w punkcie A oraz oś Oy w punkcie B . Oblicz współrzędne wszystkich punktów C leżących na osi Ox i takich, że trójkąt ABC ma pole równe 35 .
Treść dostępna po opłaceniu abonamentu.Dany jest trapez, w którym podstawy mają długość 4 cm i 10 cm oraz ramiona tworzą z dłuższą podstawą kąty o miarach 30° i 45° . Oblicz wysokość tego trapezu.
Treść dostępna po opłaceniu abonamentu.
Dany jest wielomian \(W(x) = {x^3} – 5{x^2} – 9x + 45.\)
a) Sprawdź, czy punkt A = (1, 30) należy do wykresu tego wielomianu.
b) Zapisz wielomian W w postaci iloczynu trzech wielomianów stopnia pierwszego.
Oblicz najmniejszą i największą wartość funkcji kwadratowej f (x) = (2x +1)(x − 2) w przedziale \(\left\langle { – 2,2} \right\rangle .\)
Treść dostępna po opłaceniu abonamentu.
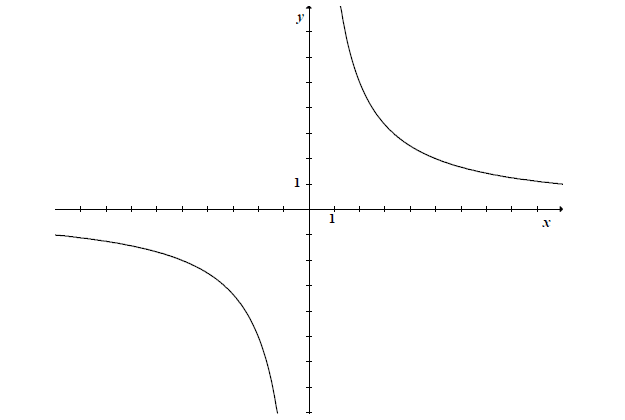
Rysunek przedstawia fragment wykresu funkcji h , określonej wzorem \(h\left( x \right) = \frac{a}{x}\quad dla\;x \ne 0\).
Wiadomo, że do wykresu funkcji h należy punkt P = (2,5).
a) Oblicz wartość współczynnika a .
b) Ustal, czy liczba h(π) − h(−π) jest dodatnia czy ujemna.
c) Rozwiąż nierówność h( x) > 5.
 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Pole powierzchni bocznej ostrosłupa prawidłowego trójkątnego równa się \(\frac{{{a^2}\sqrt {15} }}{4}\) gdzie a oznacza długość krawędzi podstawy tego ostrosłupa. Zaznacz na poniższym rysunku kąt nachylenia ściany bocznej ostrosłupa do płaszczyzny jego podstawy. Miarę tego kąta oznacz symbolem β . Oblicz cosβ i korzystając z tablic funkcji trygonometrycznych odczytaj przybliżoną wartość β z dokładnością do 1° .
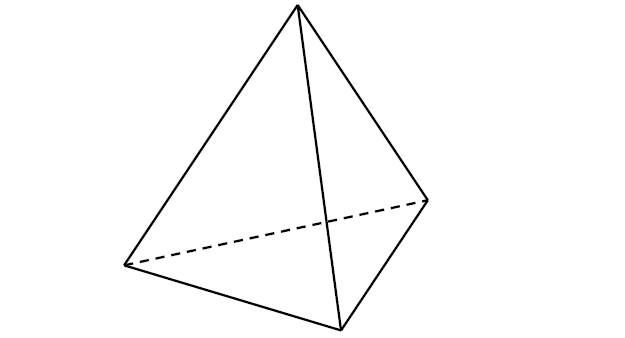 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo
każdego z następujących zdarzeń:
a) A – w każdym rzucie wypadnie nieparzysta liczba oczek.
b) B – suma oczek otrzymanych w obu rzutach jest liczbą większą od 9.
c) C – suma oczek otrzymanych w obu rzutach jest liczbą nieparzystą i większą od 9.
- Matura z matematyki 2017 – Maj podstawowa
- Matura z matematyki 2016 – Maj podstawowa
- Matura z matematyki 2015 – Maj podstawowa
- Matura z matematyki 2014 – Maj podstawowa
- Matura z matematyki 2013 – Maj podstawowa
- Matura z matematyki 2012 – Maj podstawowa
- Matura z matematyki 2011 – Maj podstawowa
- Matura z matematyki 2010 – Maj podstawowa
- Matura z matematyki 2009 – Maj podstawowa
- Matura z matematyki 2008 – Maj podstawowa
- Matura z matematyki 2007 – Maj podstawowa
- Matura z matematyki 2006 – Maj podstawowa
- Matura z matematyki 2005 – Maj podstawowa
- Matura z matematyki 2003 – Maj podstawowa




