Stożek – zadania
Zobacz najważniejsze zadania pokazujące krok po kroku – jak obliczyć objętość i pole całkowite stożka? Nie przegap głównych zadań, które mogą pojawić się w gimnazjum i liceum na sprawdzianie, egzaminie lub maturze z matematyki.
Objętość stożka i pole całkowite – rozwiązania zadań
Oblicz pole całkowite i objętość stożka powstałego w wyniku obrotu trójkąta prostokątnego o przyprostokątnych 3 i 2 wokół krótszej przyprostokątnej.

Zadanie ćwiczy wykorzystanie wzorów na objętość i pole całkowite stożka. Do obliczenia pola całkowitego stożka należy najpierw wyznaczyć pole podstawy stożka oraz jego pole boczne.
Warto tutaj przypomnieć, że wzór na pole boczne stożka: \({{P}_{b}}=\pi \cdot r\cdot l\) można zapamiętać przez skrót: Polska Rzeczpospolita Ludowa – PRL.
Mi to pomaga, więc Tobie również polecam.
Przekrój stożka jest trójkątem równobocznym o wysokości \(8\sqrt{3}\). Oblicz pole całkowite tego stożka.
W tym zadaniu korzystamy z faktu, że przekrój stożka jest trójkątem równobocznym. Mamy wysokość stożka, a zarazem wysokość trójkąta równobocznego. Dalej przyrównujemy wzór na wysokość trójkąta równobocznego do wartości z treści zadania i obliczamy w ten sposób bok trójkąta równobocznego. Mając bok zauważamy, że to tworząca stożka, zaś promień podstawy jest 2 razy mniejszy niż tworząca. Mając już wszystkie wymiary stożka można obliczyć ze znanych wzorów pole całkowite stożka.
Oblicz promień podstawy stożka odczytując informacje z rysunku.
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Oblicz kąt \(\alpha\) odczytując potrzebne informacje z podanego rysunku.
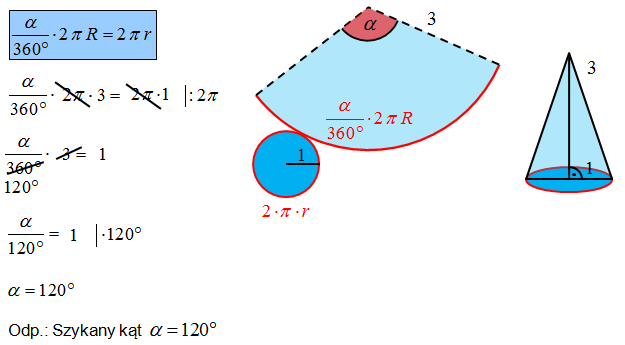
Wykorzystaj wskazówkę z poprzedniego zadania.
Treść dostępna po opłaceniu abonamentu.Dana jest wysokość stożka o długości 2. Oblicz jego objętość, jeśli kąt nachylenia tworzącej do podstawy wynosi 30 stopni.
Dość łatwo zauważyć, że połowa przekroju osiowego stożka jest bardzo charakterystycznym trójkątem o kątach 30 °, 60 ° i 90 °. Jest to zadanie, które można zrobić kilkoma sposobami. Mam tu na myśli wykorzystanie kąta 30 stopni.
- w zadaniu wykorzystuję proporcje w danym trójkącie: \(a,\ \frac{1}{2}a,\ \frac{a\sqrt{3}}{2}\)
- w literaturze można spotkać równoważne proporcje boków tego samego trójkąta: \(a,\ 2a,\ a\sqrt{3}\)
- można także wykorzystać w tym zadaniu funkcje trygonometryczne jednak uważam, że dwa poprzednie sposoby są bardziej przystępne. Oczywiście ostateczna decyzja należy do rozwiązującego zadanie i jego przyzwyczajeń.
Dana jest wysokość stożka równa 9 cm. Oblicz jego objętość i pole boczne, jeśli kąt jego rozwarcia wynosi 60 stopni.
Treść dostępna po opłaceniu abonamentu.Oblicz pole boczne stożka o objętości \(270\,\pi \ \) i wysokości 10.
Treść dostępna po opłaceniu abonamentu.



