Egzamin gimnazjalny z matematyki 2005 online
Poniższy diagram wykorzystaj do rozwiązania zadań od 1. do 4. Przyjmij, że lądy na Ziemi zajmują łącznie 150 mln km2. Diagram przedstawia procentowy udział powierzchni poszczególnych kontynentów w całkowitej powierzchni lądów.
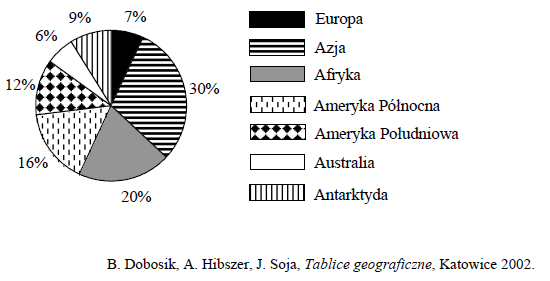
Które zdanie jest prawdziwe?
A. Ameryka Północna i Azja zajmują łącznie więcej niż połowę lądów Ziemi.
B. Europa ma najmniejszą powierzchnię spośród wszystkich kontynentów.
C. Afryka i Azja mają łącznie większą powierzchnię niż pozostałe lądy Ziemi.
D. Powierzchnia Azji stanowi mniej niż jedną trzecią powierzchni lądów Ziemi.
Jaką część powierzchni lądów na Ziemi zajmuje Afryka?
A.1/4 B.1/5 C.1/20 D.1/50
Jaką powierzchnię ma Australia?
A. 0,9 mln km2 B. 6 mln km2 C. 9 mln km2 D. 90 mln km2
Powierzchnia Antarktydy jest większa od powierzchni Europy o
A. 3 mln km2 B. 7,5 mln km2 C. 30 mln km2 D. 34,5 mln km2
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Które z naczyń w kształcie walca, o wymiarach przedstawionych na rysunku, ma największą objętość?
A. I B. II C. III D. IV
Treść dostępna po opłaceniu abonamentu.Do naczynia o objętości V = 0,75 l wlano 0,45 l wody. Jaki procent objętości tego naczynia stanowi objętość wody?
A. 6 B. 16,(6) C. 33,75 D. 60
Treść dostępna po opłaceniu abonamentu.Średnia odległość Marsa od Słońca wynosi 2,28·108 km. Odległość ta zapisana bez użycia potęgi jest równa
A. 22 800 000 km
B. 228 000 000 km
C. 2 280 000 000 km
D. 22 800 000 000 km
Informacje i tabela do zadań 28. i 29.
Most zbudowany jest z przęseł o długości 10 m każde. Przęsło pod wpływem wzrostu temperatury wydłuża się. Przyrost tego wydłużenia jest wprost proporcjonalny do przyrostu temperatury. Wartość przyrostu długości przęsła dla wybranych wartości przyrostu temperatury przedstawia poniższa tabela.
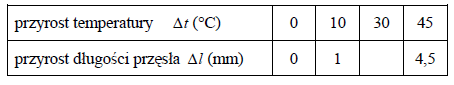
Wpisz do tabeli brakującą wartość przyrostu długości przęsła.
Treść dostępna po opłaceniu abonamentu.Zapisz zależność przyrostu długości przęsła (Δl) od przyrostu temperatury (Δt) za pomocą wzoru. Podaj współczynnik proporcjonalności Δl do Δt z odpowiednią jednostką.
wzór : …………………….
współczynnik proporcjonalności : ………………………..
Teleskop Hubble’a znajduje się na orbicie okołoziemskiej na wysokości około 600 km nad Ziemią. Oblicz wartość prędkości, z jaką porusza się on wokół Ziemi, jeżeli czas jednego okrążenia Ziemi wynosi około 100 minut. Zapisz obliczenia.
(Przyjmij Rz = 6400 km,π = 22/7 )
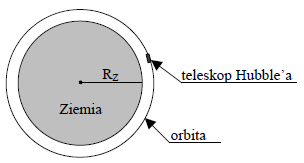Treść dostępna po opłaceniu abonamentu.
Wieża Eiffla znajduje się na obszarze w kształcie kwadratu o boku długości 125 m. Ile hektarów powierzchni ma ten obszar? Zapisz obliczenia. Wynik podaj z dokładnością do 0,1 ha.
Treść dostępna po opłaceniu abonamentu.Piramida ma kształt ostrosłupa prawidłowego czworokątnego. Ile cm2 papieru potrzeba na wykonanie modelu tej piramidy (wraz z podstawą), w którym krawędzie podstawy mają długość 10 cm a wysokość 12 cm? Ze względu na zakładki zużycie papieru jest większe o 5%. Zapisz obliczenia.
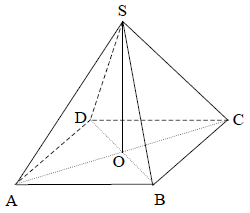Treść dostępna po opłaceniu abonamentu.
Tabela do zadania 35. zawiera ceny paliw.
| Cena benzyny | Cena gazu |
| 3,80 zł / l | 1,60 zł / l |
Montaż instalacji gazowej w samochodzie kosztuje 2208 zł. Samochód spala średnio 7 litrów benzyny lub 8 litrów gazu na każde 100 km drogi. Oblicz, po ilu miesiącach zwrócą się koszty instalacji, jeśli w ciągu miesiąca samochód przejeżdża średnio 2000 km. Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.- Egzamin gimnazjalny z matematyki 2017
- Egzamin gimnazjalny z matematyki 2016
- Egzamin gimnazjalny z matematyki 2015
- Egzamin gimnazjalny z matematyki 2014
- Egzamin gimnazjalny z matematyki 2013
- Egzamin gimnazjalny z matematyki 2012
- Egzamin gimnazjalny z matematyki 2011
- Egzamin gimnazjalny z matematyki 2010
- Egzamin gimnazjalny z matematyki 2009
- Egzamin gimnazjalny z matematyki 2008
- Egzamin gimnazjalny z matematyki 2007
- Egzamin gimnazjalny z matematyki 2006
- Egzamin gimnazjalny z matematyki 2005
- Egzamin gimnazjalny z matematyki 2004
- Egzamin gimnazjalny z matematyki 2003
- Egzamin gimnazjalny z matematyki 2002