Egzamin gimnazjalny z matematyki 2003 online
Informacja do zadań 1. i 2.
Diagram kołowy przedstawia wyniki wyborów do samorządu szkolnego.
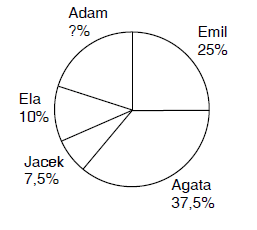
Ile procent uczniów głosowało na Adama?
A. 25 B. 20 C. 10 D. 80
Jaka część uczniów głosowała na Agatę?
A. Mniej niż 1/4ogółu.
B. Mniej niż 1/3, ale więcej niż 1/4ogółu.
C. Więcej niż 1/3, ale mniej niż 2/5ogółu.
D. Więcej niż 2/5ogółu.
1 mol to taka ilość materii, która zawiera w przybliżeniu 6·1023 (odpowiednio) atomów, cząsteczek lub jonów. Ile cząsteczek wody zawartych jest w 0,25 mola wody?
A. 1,5·1023 B. 0,5·1022 C. 1023 D. 0,25·1023Informacje do zadań 11. i 12.

Jeżeli struś ma masę 100 kg, a kura masę 1 kg, to zgodnie z tabelą różnica mas ich jaj wyrażona w gramach jest równa
A. 3 B. 96 C. 99 D. 960
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Które zdanie o zależności czasu inkubacji od masy ciała ptaka jest prawdziwe?
A. Czas inkubacji jest wprost proporcjonalny do masy ciała ptaka.
B. Czas inkubacji rośnie wraz ze wzrostem masy ciała ptaka.
C. Czas inkubacji jest odwrotnie proporcjonalny do masy ciała ptaka.
D. Czas inkubacji maleje wraz ze wzrostem masy ciała ptaka.
Jajo strusia jest około 3 razy dłuższe od jaja kury. Jeżeli założyć, że żółtka tych jaj mają kształt kul podobnych w skali 3 : 1, to żółtko w strusim jaju ma objętość większą, niż żółtko w jaju kurzym
A. 27 razy. B. 9 razy. C. 6 razy. D. 3 razy.
Treść dostępna po opłaceniu abonamentu.Informacje do zadań 14. i 15.
Owoce zbóż nazywamy ziarniakami. Na rysunkach przedstawiono przekroje podłużne przez jajo kury i ziarniak kukurydzy.
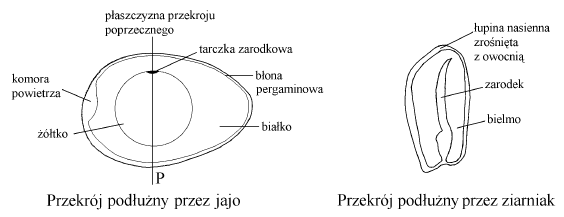
Który z rysunków: I, II, III czy IV przedstawia przekrój poprzeczny przez jajo kury wykonany w miejscu zaznaczonym linią P?
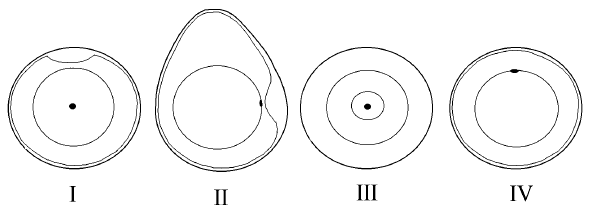
A. I B. II C. III D. IV
Treść dostępna po opłaceniu abonamentu.Informacje do zadań: 19 – 21.
Oto wyniki krótkiego sprawdzianu przeprowadzonego w trzech oddziałach II klasy gimnazjum:
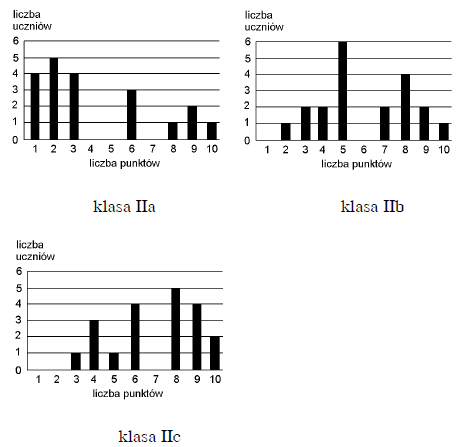
Z porównania wykresów wynika, że sprawdzian był
A. najtrudniejszy dla uczniów z IIa.
B. najtrudniejszy dla uczniów z IIb.
C. najtrudniejszy dla uczniów z IIc.
D. jednakowo trudny dla uczniów z oddziałów a, b i c.
Średni wynik uczniów z IIb jest równy 6 punktów. Ilu uczniów w tej klasie uzyskało taki wynik?
A. 0 B. 1 C. 3 D. 4
Treść dostępna po opłaceniu abonamentu.Ilu uczniów z klasy IIa otrzymało co najmniej 6 punktów?
A. 13 B. 7 C. 4 D. 3
Treść dostępna po opłaceniu abonamentu.Pan Jan wpłacił 1200 zł do banku FORTUNA, w którym oprocentowanie wkładów oszczędnościowych jest równe 8% w stosunku rocznym. Ile wyniosą odsetki od tej kwoty po roku, a ile złotych pozostanie z nich panu Janowi, jeśli od kwoty odsetek zostanie odprowadzony podatek 20%? Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.Informacje do zadań: 27 – 30.
Obserwując zużycie benzyny w swoim samochodzie, pan Nowak stwierdził, że jeżeli wystartuje z pełnym bakiem i będzie jechał po autostradzie ze stałą prędkością, to zależność liczby litrów benzyny w baku (y) od liczby przejechanych kilometrów (x) wyraża się wzorem:
y = – 0,05x + 45
Ile benzyny zostanie w baku po przejechaniu 200 km? Zapisz obliczenia
Treść dostępna po opłaceniu abonamentu.Na przejechanie ilu kilometrów wystarczy pełny bak? Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.Przekształcając wzór pana Nowaka, wyznacz x w zależności od y.
Treść dostępna po opłaceniu abonamentu.Ewa usiadła na ławce w odległości 6 m od domu Adama. Odbity od kałuży słoneczny promień poraził ją w oczy. To Adam z okna swego pokoju przesłał Ewie „zajączka”. Oblicz, na jakiej wysokości Adam błysnął lusterkiem, jeżeli promień odbił się w odległości 0,75 metra od Ewy, a jej oczy znajdowały się na wysokości 1 metra nad ziemią. Zrób rysunek pomocniczy. Zapisz obliczenia.
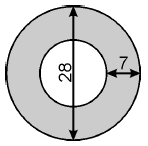
Treść dostępna po opłaceniu abonamentu.Na miejscu dawnego skrzyżowania postanowiono wybudować rondo, którego wymiary (w metrach) podane są na rysunku. Oblicz, na jakiej powierzchni trzeba wylać asfalt (obszar zacieniowany na rysunku). W swoich obliczeniach za Π podstaw 22/7. Zapisz obliczenia.
 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
W czasie prac wykopaliskowych wydobyto 45m2ziemi, z której usypano kopiec w kształcie stożka. Jego pole podstawy jest równe 54m2. Oblicz wysokość kopca, pamiętając, że objętość stożka jest równa jednej trzeciej iloczynu pola podstawy i wysokości. Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.- Egzamin gimnazjalny z matematyki 2017
- Egzamin gimnazjalny z matematyki 2016
- Egzamin gimnazjalny z matematyki 2015
- Egzamin gimnazjalny z matematyki 2014
- Egzamin gimnazjalny z matematyki 2013
- Egzamin gimnazjalny z matematyki 2012
- Egzamin gimnazjalny z matematyki 2011
- Egzamin gimnazjalny z matematyki 2010
- Egzamin gimnazjalny z matematyki 2009
- Egzamin gimnazjalny z matematyki 2008
- Egzamin gimnazjalny z matematyki 2007
- Egzamin gimnazjalny z matematyki 2006
- Egzamin gimnazjalny z matematyki 2005
- Egzamin gimnazjalny z matematyki 2004
- Egzamin gimnazjalny z matematyki 2003
- Egzamin gimnazjalny z matematyki 2002




