Egzamin gimnazjalny z matematyki 2002 online
Uwaga: Poniżej zobaczysz egzamin gimnazjalny z matematyki 2002. Zadania zostały wybrane z zadań matematyczno – przyrodniczych.
Przypominam, że w 2002 roku zadania matematyczne były wymieszane z zadaniami z innych przedmiotów ścisłych.
Zadania z egzaminu gimnazjalnego 2002
Wśród gimnazjalistów przeprowadzono ankietę na temat ich zainteresowań.
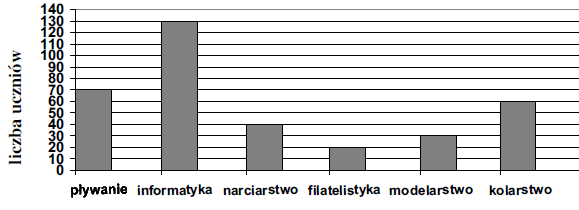
Wiedząc, że każdy uczeń podał tylko jeden rodzaj zainteresowań, rozwiąż zadania 1 – 3.
Ilu uczniów brało udział w ankiecie?
A. 250 B. 320 C. 350 D.370
O ilu mniej uczniów interesuje się kolarstwem, niż informatyką?
A. 70 B. 110 C. 120 D. 130
Ile procent wszystkich uczniów interesuje się pływaniem?
A. 5% B. 20% C. 50% D. 70%
Jacek i Paweł zbierają znaczki. Jacek ma o 30 znaczków więcej niż Paweł. Razem mają 350 znaczków. Ile znaczków ma Paweł?
A. 145 B. 160 C. 190 D. 205
Paweł kupił australijski znaczek i 3 znaczki krajowe. Każdy znaczek krajowy kosztował tyle samo. Za wszystkie znaczki zapłacił 16 zł. Ile kosztował znaczek australijski, jeżeli był pięciokrotnie droższy niż znaczek krajowy?
A. 4 zł B. 10 zł C. 12 zł D. 13 zł
Zamieszczona obok figura ma:
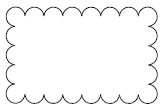
A. dokładnie 4 osie symetrii i ma środek symetrii
B. co najmniej 4 osie symetrii i nie ma środka symetrii
C. dokładnie 2 osie symetrii i nie ma środka symetrii
D. dokładnie 2 osie symetrii i ma środek symetrii
Podczas pobytu w miejscowości górskiej Adam wypożyczył narty w wypożyczalni SUPER, a Bartek w wypożyczalni EKSTRA.
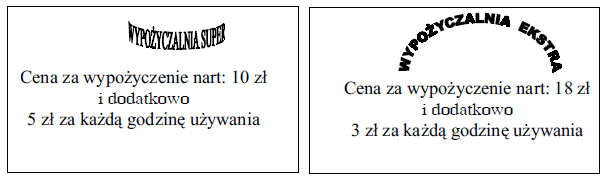
Koszt wypożyczenia nart w obu firmach będzie taki sam, jeżeli chłopcy będą używać nart przez:
A. 4 godziny B. 6 godzin C. 8 godzin D. 10 godzin
Rysunek przedstawia ślad na śniegu, który pozostawił jadący na nartach Adam.
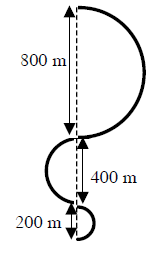
Długość trasy przebytej przez Adama równa jest:
A. 350Π m B. 700Π m C. 1400Π m D. 2100Π m
Pasją Filipa są komputery. Filip wie, że elementarną jednostką informacji jest bit. Jeden bit informacji jest kodowany jedną z dwóch wartości 0 lub 1. Dwóm bitom odpowiadają cztery możliwości: 00, 01, 10, 11. Ile możliwości odpowiada trzem bitom?
A. 2 B. 4 C. 6 D. 8
Dorota stworzyła bazę danych o krajach azjatyckich. Zamieściła w niej następujące informacje na temat Mongolii:
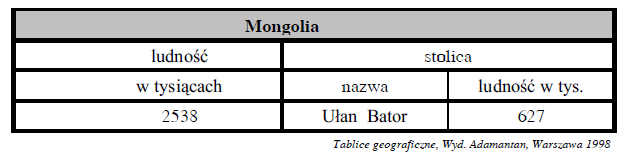
W stolicy Mongolii mieszka:
A. prawie co drugi mieszkaniec Mongolii
B. prawie co czwarty mieszkaniec Mongolii
C. prawie co dziesiąty mieszkaniec Mongolii
D. prawie co trzysta czterdziesty mieszkaniec Mongolii
Do pracowni komputerowej zakupiono 8 nowych monitorów i 6 drukarek za łączną kwotę 9400 zł. Drukarka była o 300 zł tańsza niż monitor. Cenę monitora można obliczyć, rozwiązując równanie:
A. 8x + 6(x + 300) = 9400
B. 8x + 6(x – 300) = 9400
C. 8(x-300) + 6x = 9400
D. 8(x + 300) + 6(x-300) = 9400
Akwarium, w którym Marek hoduje rybki, ma wymiary 5dm, 8dm, 6dm. Marek wlewa do niego wodę przepływającą przez kran z szybkością 8dm2 na minutę.
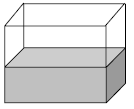
Do jakiej wysokości woda w akwarium będzie sięgać po 10 minutach. Zapisz obliczenia.
Marcin przebywa autobusem 3/4 drogi do jeziora, a pozostałą część piechotą. Oblicz odległość między domem Marcina, a jeziorem, jeżeli trasa, którą przebywa pieszo, jest o 8 km krótsza niż trasa, którą przebywa autobusem. Zapisz obliczenia.
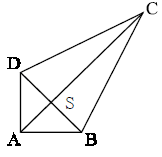
Przed przystąpieniem do budowy latawca Janek rysuje jego model. Model ten przedstawiono na rysunku w skali 1:10. Oblicz pole powierzchni latawca zbudowanego przez Janka, wiedząc, że długości odcinków AC i BD równe są odpowiednio 4cm i 2cm, oraz AC⊥BD i S – środek BD. Zapisz obliczenia.
Na zabawę karnawałową Beata wykonała kartonowe czapeczki w kształcie brył narysowanych poniżej:
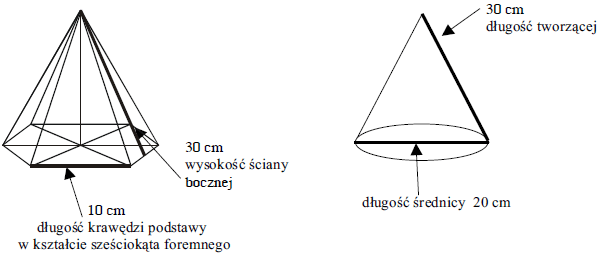
Ile papieru zużyła na każdą z czapeczek? Na którą czapeczkę zużyła więcej papieru? Zapisz obliczenia.
- Egzamin gimnazjalny z matematyki 2017
- Egzamin gimnazjalny z matematyki 2016
- Egzamin gimnazjalny z matematyki 2015
- Egzamin gimnazjalny z matematyki 2014
- Egzamin gimnazjalny z matematyki 2013
- Egzamin gimnazjalny z matematyki 2012
- Egzamin gimnazjalny z matematyki 2011
- Egzamin gimnazjalny z matematyki 2010
- Egzamin gimnazjalny z matematyki 2009
- Egzamin gimnazjalny z matematyki 2008
- Egzamin gimnazjalny z matematyki 2007
- Egzamin gimnazjalny z matematyki 2006
- Egzamin gimnazjalny z matematyki 2005
- Egzamin gimnazjalny z matematyki 2004
- Egzamin gimnazjalny z matematyki 2003
- Egzamin gimnazjalny z matematyki 2002




