Egzamin gimnazjalny z matematyki 2007 online
Informacje do zadań 1. – 6.
Zasolenie morza określa się jako ilość gramów soli rozpuszczonych w jednym kilogramie wody morskiej i podaje w promilach (‰). Przeciętnie w jednym kilogramie wody morskiej znajduje się 34,5 g różnych rozpuszczonych w niej soli (czyli przeciętne zasolenie wody morskiej jest równe 34,5‰). Zasolenie Bałtyku (średnio 7,8‰) jest znacznie mniejsze od zasolenia oceanów, co tłumaczy się wielkością zlewiska (duży dopływ wód rzecznych), warunkami klimatycznymi (małe parowanie) oraz utrudnioną wymianą wód z oceanem.
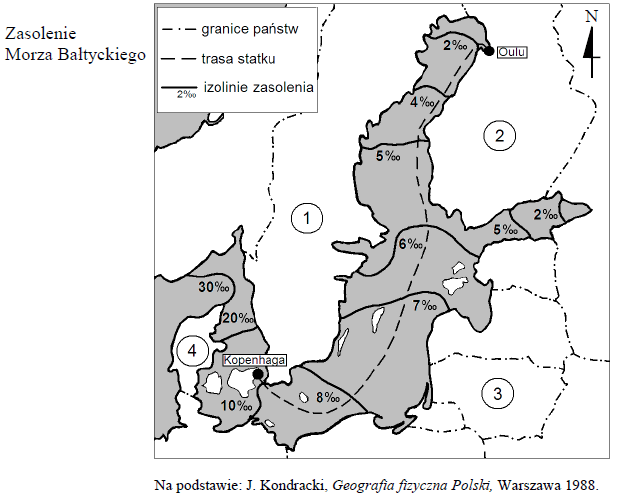
Jedna tona średnio zasolonej wody z Morza Bałtyckiego zawiera około
A. 0,078 kg soli. B. 0,78 kg soli. C. 7,8 kg soli. D. 78 kg soli.
Długość trasy na mapie w skali 1 : 10 000 000 jest równa 7,7 cm. W rzeczywistości trasa ta ma długość
A. 7,7 km B. 77 km C. 770 km D. 7700 km
Informacje do zadań 9. i 10.
Na rysunkach przedstawiono flagi sygnałowe Międzynarodowego Kodu Sygnałowego używanego do porozumiewania się na morzu.
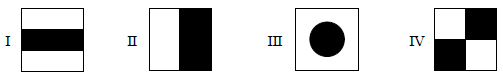
Który z przedstawionych rysunków flag ma 4 osie symetrii?
A. I B. II C. III D. IV
Który z przedstawionych rysunków flag nie ma środka symetrii?
A. I B. II C. III D. IV
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Informacje do zadań 11. i 12.
Poważnym problemem są zanieczyszczenia Bałtyku substancjami biogennymi. Diagramy przedstawiają procentowy udział państw nadbałtyckich w zanieczyszczeniu Morza Bałtyckiego związkami azotu (diagram a) i związkami fosforu (diagram b) w 1995 roku.
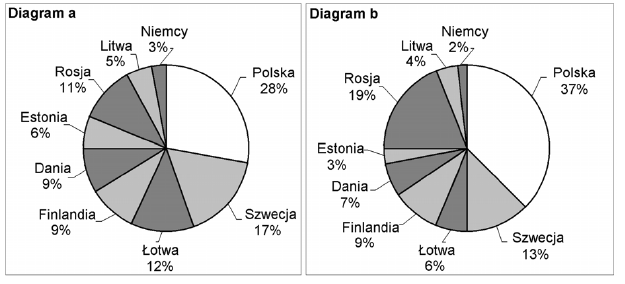
Procentowy udział Polski w zanieczyszczeniu Bałtyku związkami azotu w 1995 r. był taki, jak łącznie krajów
A. Szwecji i Rosji.
B. Rosji i Łotwy.
C. Danii i Finlandii.
D. Rosji i Finlandii.
Czworo uczniów podjęło próbę ustalenia na podstawie diagramów, czy w 1995 roku
do Bałtyku trafiło z obszaru Polski więcej ton związków azotu czy związków fosforu.
Oto ich odpowiedzi:
Bartek – Trafiło więcej ton związków fosforu.
Ewa – Trafiło więcej ton związków azotu.
Tomek – Do Bałtyku trafiło tyle samo ton związków azotu co fosforu.
Hania – Nie można obliczyć, bo brakuje danych o masie zanieczyszczeń poszczególnymi
związkami.
Kto odpowiedział poprawnie?
A. Ewa B. Tomek C. Bartek D. Hania
Treść dostępna po opłaceniu abonamentu.Informacje do zadań 17. i 18.
Rysunki przedstawiają wskazania wodomierza w dniach 1 września i 1 października.
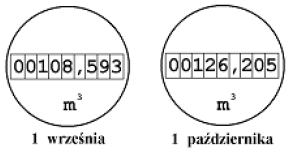
Oblicz, zaokrąglając do całości, ile metrów sześciennych wody zużyto od 1 września do 1 października.
A. 16 m3 B. 17 m3 C. 18 m3 D. 22 m3
Treść dostępna po opłaceniu abonamentu.Pierwszego października wodomierz wskazywał 126,205 m3. Jakie będzie wskazanie tego wodomierza po zużyciu kolejnych 10 litrów wody?
A. 136,205 m3 B. 127,205 m3 C. 126,305 m3 D. 126,215 m3
Treść dostępna po opłaceniu abonamentu.Objętość (V) cieczy przepływającej przez rurę o polu przekroju S oblicza się według wzoru V = Svct, gdzie vc oznacza prędkość przepływu cieczy, t – czas przepływu. Który wzór na prędkość cieczy przepływającej przez rurę jest rezultatem poprawnego przekształcenia podanego wzoru?
Treść dostępna po opłaceniu abonamentu.
Rodzice Jacka kupili 36 butelek wody mineralnej o pojemnościach 0,5 litra i 1,5 litra. W sumie zakupili 42 litry wody. Przyjmij, że x oznacza liczbę butelek o pojemności 0,5 litra, y – liczbę butelek o pojemności 1,5 litra. Który układ równań umożliwi obliczenie, ile zakupiono mniejszych butelek wody mineralnej, a ile większych?
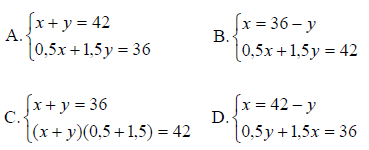Treść dostępna po opłaceniu abonamentu.
Do początkowo pustych wazonów, takich jak przedstawione na rysunkach, jednakowym i równomiernym strumieniem wpływała woda.
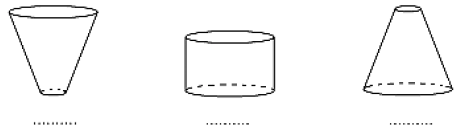
Na wykresach I – IV przedstawiono schematycznie charakter zależności wysokości poziomu wody w wazonie od czasu jego napełniania. Pod każdym wazonem wpisz numer odpowiedniego wykresu.
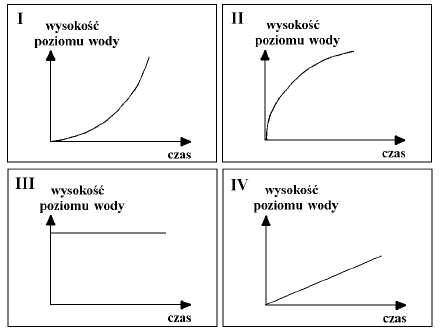Treść dostępna po opłaceniu abonamentu.
W wiadrze jest x litrów wody, a w garnku y litrów wody. Ile litrów wody będzie w wiadrze, a ile w garnku, jeśli:
1. z wiadra przelejemy do garnka 1,5 litra wody;
2. przelejemy połowę wody z garnka do wiadra?
Wpisz do tabeli odpowiednie wyrażenia algebraiczne.
Treść dostępna po opłaceniu abonamentu.
Informacje do zadań 32. i 33.
Przekrój poprzeczny ziemnego wału przeciwpowodziowego ma mieć kształt równoramiennego trapezu o podstawach długości 6 m i 16 m oraz wysokości 12 m. Trzeba jednak usypać wyższy wał, bo przez dwa lata ziemia osiądzie i wysokość wału zmniejszy się o 20% (szerokość wału u podnóża i na szczycie nie zmienia się).
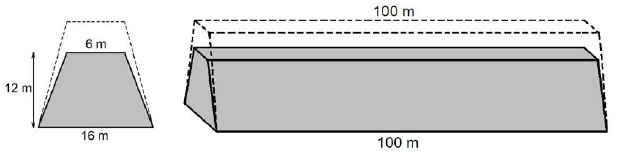
Oblicz, ile metrów sześciennych ziemi trzeba przywieźć na usypanie 100-metrowego odcinka ziemnego wału przeciwpowodziowego (w kształcie graniastosłupa prostego) opisanego w informacjach. Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.Po zakończeniu osiadania ziemi, w celu zmniejszenia przesiąkania, na zboczu wału od strony wody zostanie ułożona warstwa gliny. Oblicz pole powierzchni, którą trzeba będzie wyłożyć gliną na 100-metrowym odcinku tego wału (wał ma kształt graniastosłupa prostego). Zapisz obliczenia. Wynik podaj z jednostką.
Treść dostępna po opłaceniu abonamentu.
- Egzamin gimnazjalny z matematyki 2017
- Egzamin gimnazjalny z matematyki 2016
- Egzamin gimnazjalny z matematyki 2015
- Egzamin gimnazjalny z matematyki 2014
- Egzamin gimnazjalny z matematyki 2013
- Egzamin gimnazjalny z matematyki 2012
- Egzamin gimnazjalny z matematyki 2011
- Egzamin gimnazjalny z matematyki 2010
- Egzamin gimnazjalny z matematyki 2009
- Egzamin gimnazjalny z matematyki 2008
- Egzamin gimnazjalny z matematyki 2007
- Egzamin gimnazjalny z matematyki 2006
- Egzamin gimnazjalny z matematyki 2005
- Egzamin gimnazjalny z matematyki 2004
- Egzamin gimnazjalny z matematyki 2003
- Egzamin gimnazjalny z matematyki 2002