Egzamin gimnazjalny 2015 z matematyki
Egzamin gimnazjalny z matematyki 2015 stał się faktem i pokazał, że zadania były bardzo proste, za wyjątkiem kilku podchwytliwych jak zadania z lodem 🙂 Zobacz arkusze i odpowiedzi w filmach do egzaminu. Będzie to zarazem idealna powtórka do przyszłorocznego testu gimnazjalnego.
Egzamin gimnazjalny z matematyki 2015 – arkusz i rozwiązania
- Egzamin gimnazjalny z matematyki 2015 – Arkusz CKE
Informacje do zadań 1 i 2
Każda z dwóch kolejek górskich przebywa drogę 150 metrów w ciągu minuty. Na schemacie zaznaczono niektóre długości trasy pokonywanej przez kolejki.
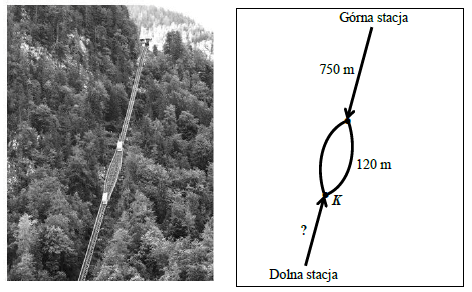 Zadanie 1. (0–1)
Zadanie 1. (0–1)
Jak długo trwa przejazd kolejki od górnej stacji do punktu K? Wybierz właściwą odpowiedź spośród podanych.
Rozwiązanie:
Informacje do zadań 1 i 2
Każda z dwóch kolejek górskich przebywa drogę 150 metrów w ciągu minuty. Na schemacie zaznaczono niektóre długości trasy pokonywanej przez kolejki.
Zadanie 2. (0–1)Z górnej stacji kolejka wyjeżdża o 1 minutę wcześniej niż z dolnej. Kolejki równocześnie wjeżdżają na pętlę mijania.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Długość trasy od dolnej stacji do punktu K jest równa
Rozwiązanie:
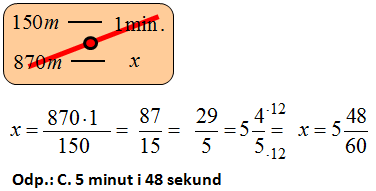
Droga pokonana przez kolejkę górną w ciągu 1 minuty to 150m. Stąd nalezy zauważyć, że trasa kolejki dolnej jest krótsza właśnie o tę odległość. Zatem 750-150=600m
Odp.: C. 600 m
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Na osi liczbowej liczba wartości wyrażenia arytmetycznego \(\big(1- \frac{5}{6} \big) -0,5\) znajduje się między
Rozwiązanie:
Obliczamy wartość arytmetycznego i zaznaczamy tę liczbe na osi liczbowej
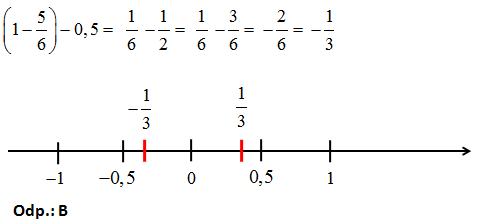
Dane jest przybliżenie \(\sqrt{5}\approx 2,236.\)
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli zdanie jest fałszywe.
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Rozwiązanie:
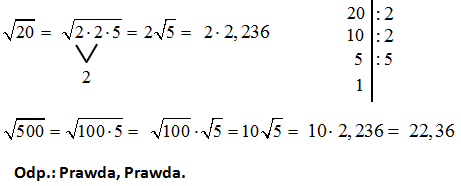
Poniżej podano kilka kolejnych potęg liczby 7.
71 = 7
72 = 49
73 = 343
74 = 2401
75 = 16 807
76 = 117 649
77 = 823 543
78 = 5 764 801
79 = 40 353 607
…………….
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Cyfrą jedności liczby 7190 jest
Rozwiązanie:
Należy zauważyć, ze ostatnie cyfry powtarzają się okresowo: 7,9,3,1,7,9,3,1,7,9,3,1,……itd. Zatem co czwarta potęga (ta z wykładnikiem podzielnym przez 4 ma na końcu cyfrę 1). Tym sposobem obliczamy 7188=…1, a kolejne potęgi powtarzają się w okresie 7,9,3,1. Dlatego 7189=…7, 7190=…9.
Odp.: D=9.
W dodatniej liczbie trzycyfrowej cyfra dziesiątek jest równa 5, a cyfra setek jest o 6 mniejsza od cyfry jedności.
Ile jest liczb spełniających te warunki? Wybierz właściwą odpowiedź spośród podanych.
Rozwiązanie:
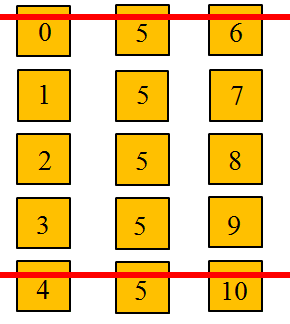
Warto zacząć od uzupełnienia cyfry dziesiątek przez cyfrę 5. Dalej należy uzupełniać miejsca setek począwszy od możliwie najmniejszych cyfr. Do każdej cyfry setek należy dobrać o 6 większą cyfrę jedności. Pamiętaj, aby nie przekroczyć największej cyfry 9. Bo liczba 10 to liczba, a nie cyfra.
Odp.: C- trzy.
Zmieszano dwa gatunki herbaty, droższą i tańszą, w stosunku 2:3. Cena jednego kilograma tej herbacianej mieszanki wynosi 100 zł. Gdyby ty herbaty zmieszano w stosunku 1:4, to cena za 1 kg tej mieszanki wynosiła by 80 zł. Na podstawie podanych informacji zapisano poniższy układ równań.
\(\left\{ \begin{matrix} \frac{2}{5}x+\frac{3}{5}y=110 \\ \frac{1}{5}x+\frac{4}{5}y=80 \\ \end{matrix} \right.\)Co oznacza x w tym układzie równań? Wybierz właściwą odpowiedź spośród podanych.
Rozwiązanie:
Obejrzyj film z wytłumaczeniem.
Odp.: A. Cenę 1 kg herbaty droższej.
Na wykresie przedstawiono, jak zmienia się masa porcji lodów z wafelkiem w zależności od liczby gałek lodów.
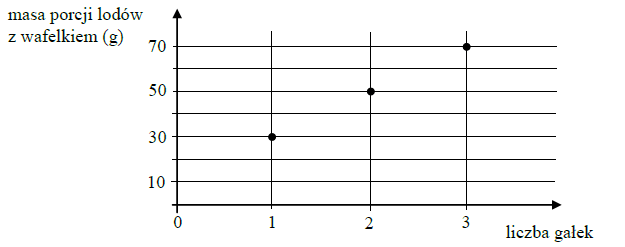
Jaką masę ma jedna gałka tych lodów bez wafelka? Wybierz właściwą odpowiedź spośród podanych.
Rozwiązanie:
MOżna zauważyć, że różnica między masą lodów z dwiema gałkami, a masą z jedną gałką lodu to 50-30=20g. Stąd gałka waży 20g.
Odp.: B. 20g
W konkursie przyznano nagrody pieniężne. Zdobywca pierwszego miejsca otrzymał 5000zł. Nagroda za zdobycie drugiego miejsca była o 30% mniejsza niż nagroda za zajęcie pierwszego miejsca. Nagroda za zdobycie trzeciego miejsca była o 40% mniejsza, niż nagroda za zajęcie drugiego miejsca.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli zdanie jest fałszywe.
 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Rozwiązanie:

Odp.: Fałsz, Fałsz.
Doświadczenie losowe polega na dwukrotnym rzucie monetą. Jeśli wypadnie orzeł, zapisujemy 1, a jeśli reszka – zapisujemy 2. Wynikiem doświadczenia jest zapisana liczba dwucyfrowa.
Jakie jest prawdopodobieństwo, że zapisana liczba jest podzielna przez 3? Wybierz właściwą odpowiedź spośród podanych.
Rozwiązanie:
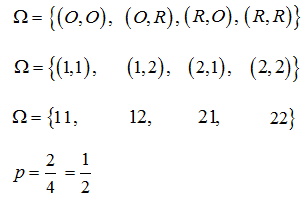
Odp.: D. \(\frac{1}{2}\)
Pięć różnych liczb naturalnych zapisano w kolejności od najmniejszej do największej: 1, a, b, c, 10. Mediana liczb: 1, a, b jest równa 3, a mediana liczb: a, b, c, 10 jest równa 5.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba c jest równa
Rozwiązanie:
Mediana to wartość środkowa w ciągu uporzadkowanym. Jeśli ciąg ma parzystą liczbę wyrazów to medianą jest średnia arytmetyczna dwóch środkowych wyrazów tego uporządkowanego ciągu.
Dany jest ciąg uporządkowany: 1, a, b, c, 10.
Wiemy, że medianą liczb: 1, a, b jest równa 3. Stąd możemy wywnioskować, że a=3.
Mamy ciąg uporządkowany: 1, a, b, c, 10. Wiedząc, że a=3 otrzymujemy ciąg liczb: 1, 3, b, c, 10.
Z zadania wiemy, że mediana liczb: 3, b, c, 10 jest równa 5.
Zatem b=4, c=6, ponieważ mediana liczb: 3, 4, 6, 10 jest równa 5, ponieważ średnia dwóch środkowychwyrazów 4 i 6 jest równa 5.
Inne możliwości są niedopuszczalne, ponieważ psują nam początkowe warunki zadania o rosnąco uporządkownych liczbach oraz o niepowtarzalności liczb w ciągu.
Odp.: C. 6
Liczba x jest dodatnia, a liczba y jest ujemna.
Ile spośród liczb: \(x\cdot y,\ \ x-y,\ \ \frac{x}{y},\ \ {{\left( y-x \right)}^{2}}\) jest dodatnich? Wybierz właściwą odpowiedź spośród podanych.
Rozwiązanie:
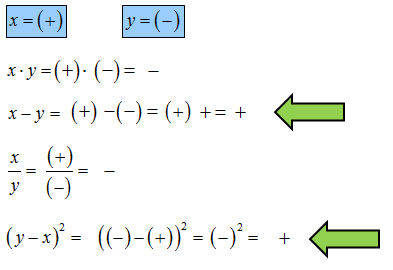
Odp.: B. Dwie
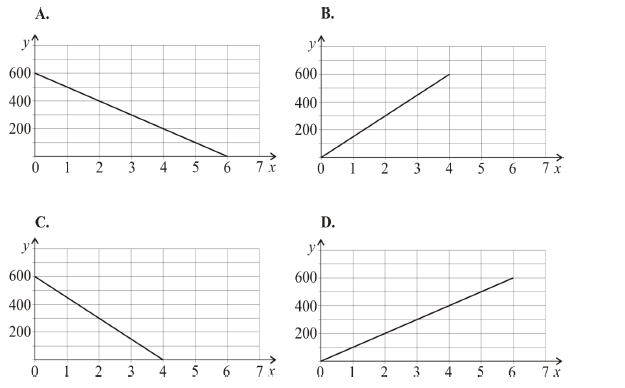
Wzór y = 600 – 100x opisuje zależność objętości y (w litrach) wody w zbiorniku od czasu x (w minutach) upływającego podczas opróżniania tego zbiornika.
Który wykres przedstawia tę zależność? Wybierz właściwą odpowiedź spośród podanych.
 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Rozwiązanie:
Do wzoru funkcji y = 600 – 100x wstawiamy kolejno argumenty x=0, a następnie x=4. Odpowiednio po wykorzystaniu wzoru funkcji otrzymujemy wartości funkcji: y=600 oraz y=200. Stąd mamy pary liczb: (0,600) i (4,200), które są jednocześnie współrzędnymi dwóch punktów. Widać, że oba te punkty należą tylko do wykresu A.
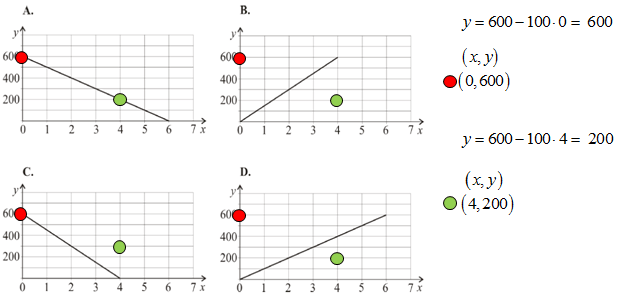
Odp.: A.
Jeżeli a, b i c są długościami boków trójkąta oraz c jest najdłuższym bokiem, to ten trójkąt jest:
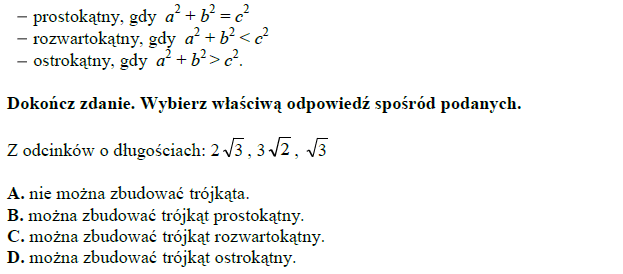 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Proste m i n są styczne do okręgu i przecinają się pod kątem 30°.
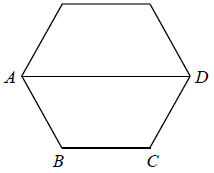
Treść dostępna po opłaceniu abonamentu.Na rysunku przedstawiono sześciokąt foremny o boku równym 2 cm. Przekątna AD dzieli go na dwa przystające trapezy równoramienne.
 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Ania wycięła z kartki papieru dwa jednakowe trójkąty prostokątne o bokach długości 12 cm, 16 cm i 20 cm. Pierwszy z nich zagięła wzdłuż symetralnej krótszej przyprostokątnej, a drugi – wzdłuż symetralnej dłuższej przyprostokątnej. W ten sposób otrzymała czworokąty pokazane na rysunkach.
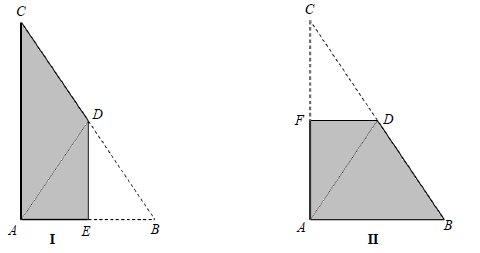 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Rysunki przedstawiają bryłę, której wszystkie cztery ściany są trójkątami równobocznymi.
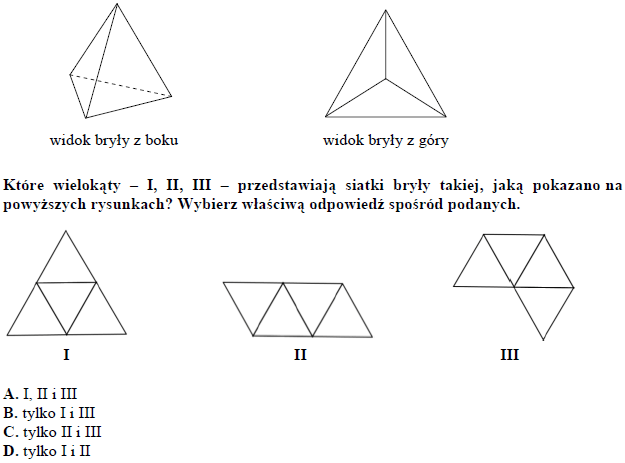 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Szklane naczynie w kształcie prostopadłościanu o wymiarach 6 cm, 15 cm i 18 cm napełniono częściowo wodą i szczelnie zamknięto. Następnie naczynie postawiono na jego ścianie o największej powierzchni i wtedy woda sięgała do wysokości 4 cm. Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Kiedy naczynie postawiono na ścianie o najmniejszej powierzchni, to woda sięgała do wysokości
Treść dostępna po opłaceniu abonamentu.Na rysunku przedstawiono ostrosłup prawidłowy czworokątny i sześcian. Bryły mają jednakowe podstawy i równe wysokości, a suma objętości tych brył jest równa 36 cm3.
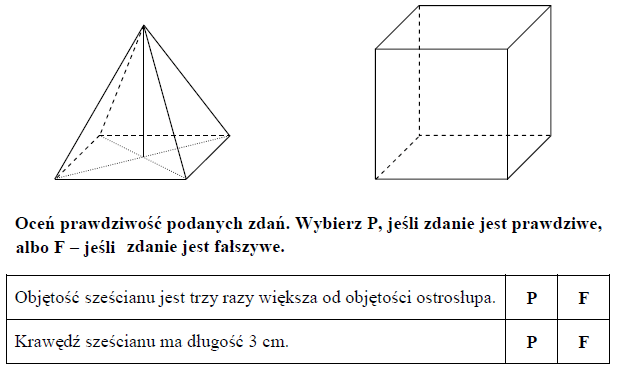 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Maja, Ola i Jagna kupowały zeszyty. Maja za 3 grube zeszyty i 8 cienkich zapłaciła 10 zł. Ola kupiła 4 grube oraz 4 cienkie zeszyty i również zapłaciła 10 zł. Czy Jagnie wystarczy 10 złotych na zakup 5 grubych zeszytów i 1 cienkiego? Zapisz obliczenia i odpowiedź.
Treść dostępna po opłaceniu abonamentu.Przekątna prostokąta ABCD nachylona jest do jednego z jego boków pod kątem 30°. Uzasadnij, że pole prostokąta ABCD jest równe polu trójkąta równobocznego o boku równym przekątnej tego prostokąta.
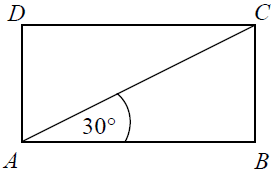 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Po rozklejeniu ściany bocznej pudełka mającego kształt walca otrzymano równoległobok. Jeden z boków tej figury ma długość 44 cm, a jej pole jest równe 220cm2. Oblicz objętość tego pudełka. Przyjmij przybliżenie π równe \(\frac{22}{7}\). Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.Egzamin gimnazjalny 2015 – matematyka. To już historia, ale warto rozwiazać wyżej wymienione zadania i wiele innych w celu trenningu. Każdy trening czyni mistrza, czy w sporcie, czy w nauce przedmiotu: matematyka. Rozwiąż jak największą liczbę zadań przed nadchodzącym egzaminem gimnazjalnym.
Zapraszam do pozostałych egzaminów z poprzednich lat oraz informacji jak dobrze przygotować się do egzaminu gimnazjalnego.
- Egzamin gimnazjalny z matematyki 2017
- Egzamin gimnazjalny z matematyki 2016
- Egzamin gimnazjalny z matematyki 2015
- Egzamin gimnazjalny z matematyki 2014
- Egzamin gimnazjalny z matematyki 2013
- Egzamin gimnazjalny z matematyki 2012
- Egzamin gimnazjalny z matematyki 2011
- Egzamin gimnazjalny z matematyki 2010
- Egzamin gimnazjalny z matematyki 2009
- Egzamin gimnazjalny z matematyki 2008
- Egzamin gimnazjalny z matematyki 2007
- Egzamin gimnazjalny z matematyki 2006
- Egzamin gimnazjalny z matematyki 2005
- Egzamin gimnazjalny z matematyki 2004
- Egzamin gimnazjalny z matematyki 2003
- Egzamin gimnazjalny z matematyki 2002





