Monotoniczność funkcji kwadratowej
Funkcja kwadratowa nie jest rosnąca, malejąca, ani stała. Jest niemonotoniczna lub inaczej mówiąc jest monotoniczna przedziałami.
Przykład.
Podaj przedziały monotoniczności funkcji kwadratowej: \(y={{x}^{2}}-4x+8\)
Do wyznaczenia przedziałów monotoniczności należy wyznaczyć współrzędne wierzchołka paraboli, a w zasadzie tylko współrzędną x-ową.
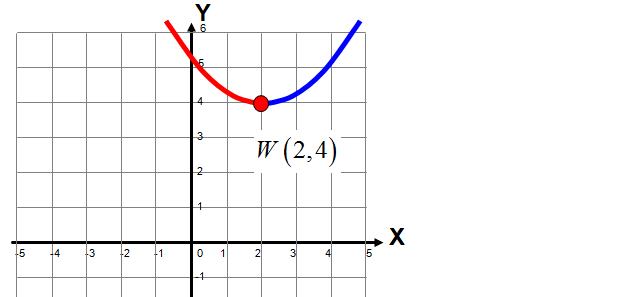 Funkcja jest malejąca w przedziale \(\left( -\infty ,\left. 2 \right\rangle \right.\)
Funkcja jest malejąca w przedziale \(\left( -\infty ,\left. 2 \right\rangle \right.\)
Funkcja jest rosnąca w przedziale \(\left\langle 2,\left. +\infty \right) \right.\)
Badanie monotoniczności funkcji kwadratowej
Zbadaj monotoniczność funkcji kwadratowej (tzn. określ, czy funkcja jest rosnąca, malejąca, czy stała) y = x2.
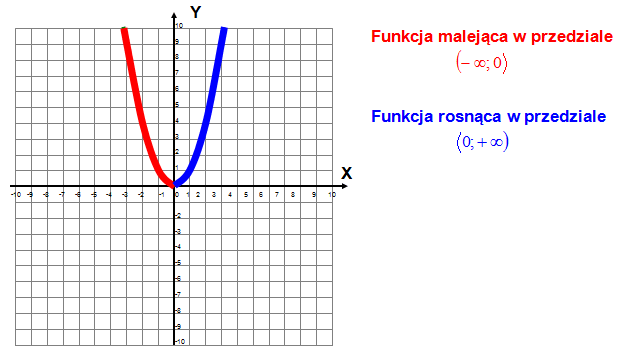
W zerze nawiasy są domknięte.
Więcej informacji o monotoniczności funkcji znajdziesz tutaj.
- Definicja funkcji kwadratowej
- Funkcja kwadratowa – wzory
- Wykres funkcji kwadratowej
- Dziedzina i zbiór wartości funkcji kwadratowej
- Monotoniczność funkcji kwadratowej
- Miejsca zerowe funkcji kwadratowej
- Postać iloczynowa trójmianu kwadratowego
- Równanie kwadratowe
- Równania kwadratowe niezupełne
- Równania sprowadzalne do równań kwadratowych
- Nierówności kwadratowe
- Funkcja kwadratowa – sprawdzian




