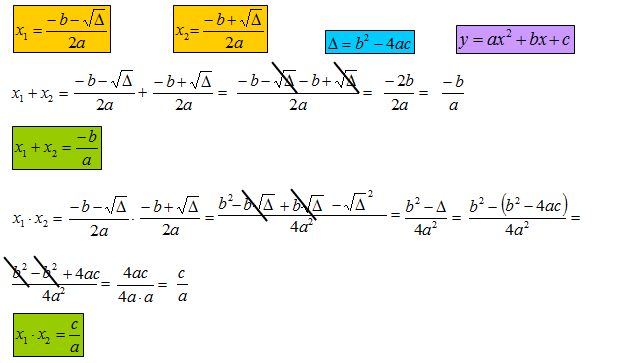Funkcja kwadratowa – wzory

Poznaj najważniejsze wzory związane z funkcją kwadratową.

Postać ogólna funkcji kwadratowej: \(y=a{{x}^{2}}+bx+c\)

Postać kanoniczna funkcji kwadratowej: \(y=a{{\left( x-p \right)}^{2}}+q\) , gdzie \(p=\frac{-b}{2a}\) i \(q=\frac{-\Delta }{4a}\)

Postać iloczynowa funkcji kwadratowej:

• jeśli Δ > 0 wówczas \(y=a\left( x-{{x}_{1}} \right)\left( x-{{x}_{2}} \right)\) , gdzie x₁ i x₂ są miejscami zerowymi
• jeśli Δ = 0 wówczas \(y=a{{\left( x-{{x}_{0}} \right)}^{2}}\) , gdzie x₀ jest jedynym miejscem zerowym
• jeśli Δ < 0 wówczas nie ma miejsc zerowych funkcji i brak postaci iloczynowej

Postać kanoniczna funkcji kwadratowej: \(y=a{{\left( x-p \right)}^{2}}+q\) , gdzie p i q to współrzędne wierzchołka paraboli \(W\ \left( p,q \right)\), gdzie \(p=\frac{-b}{2a}\) i \(q=\frac{-\Delta }{4a}\)

Wzór na wyróżnik trójmianu kwadratowego – wzór na deltę: \(\Delta ={{b}^{2}}-4\cdot a\cdot c\)

Wzory na pierwiastki trójmianu kwadratowego, czyli wzory na miejsca zerowe funkcji kwadratowej:

• jeśli Δ > 0 wówczas mamy dwa miejsca zerowe: \[{{x}_{1}}=\frac{-b-\sqrt{\Delta }}{2\cdot a}\] \[{{x}_{2}}=\frac{-b+\sqrt{\Delta }}{2\cdot a}\]
• jeśli Δ = 0 wówczas mamy jedno miejsce zerowe o wzorze: \[{{x}_{0}}=\frac{-b}{2\cdot a}\]
• jeśli Δ < 0 to brak miejsc zerowych

Wzór na wierzchołek paraboli:

\(W\ \left( p,q \right)\) jest punktem, w którym parabola ma swój wierzchołek, gdzie \[p=\frac{-b}{2a}\] \[q=\frac{-\Delta }{4a}\]

Warto tutaj również wspomnieć, że:

• jeśli współczynnik „a” przy x² jest dodatni to parabola jest skierowana ramionami do góry
• jeśli współczynnik „a” przy x² jest ujemny to parabola jest skierowana ramionami do dołu

Wzory Viete’a

Funkcja kwadratowa mająca pierwiastki rzeczywiste posiada również inne własności – wzory Viete’a.

\[{{x}_{1}}+{{x}_{2}}=-\frac{b}{a}\] \[{{x}_{1}}\cdot {{x}_{2}}=\frac{c}{a}\]

Wyprowadzenie wzorów Viete’a.

x

http://youtu.be/lF7CQGBwQhY

Zobacz na stronie

Zobacz na YouTube