Równanie kwadratowe
Równanie kwadratowe rozwiązujemy bazując na wiedzy z wyznaczania miejsc zerowych funkcji kwadratowej. Zatem, kiedy mamy dwa, kiedy jedno, a kiedy nie mamy miejsc zerowych? Oczywiście zależy to od znaku delty – patrz artykuł: Miejsca zerowe funkcji kwadratowej.
Równania kwadratowe to dość obszerny temat powiązany z funkcja kwadratową. Jeśli chcesz rozwiązać więcej równań kwadratowych, zapraszam do szerszego ich omówienia w zadaniach i przykładach.
Równania kwadratowe – Przykłady i zadania
Rozwiąż równanie kwadratowe i wykorzystaj najważniejsze wzory:
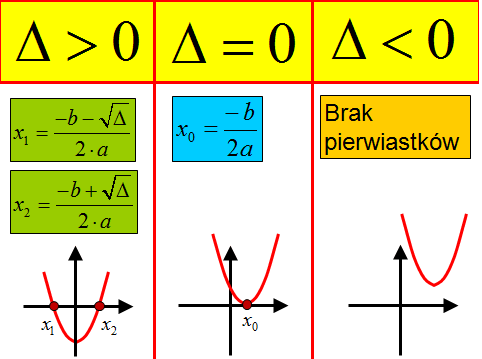
Korzystanie z wymienionych wzorów nie jest jedyną metodą rozwiązywania równań kwadratowych. Niektóre przykłady można znacznie szybciej rozwiązać korzystając, np. ze wzorów skróconego mnożenia.
Należy zauważyć, że pierwiastki równania kwadratowego są punktami przecięcia się paraboli z osią X. Jak widzisz na rysunku wyżej mogą występować jedno, dwa lub brak punktów wspólnych wykresu z osią X, a tym samym może nie być pierwiastków równania kwadratowego.
W literaturze są zazwyczaj podane wzory na dwa pierwiastki rzeczywiste, tak jak pokazuje prezentacja wyżej. Osobiście nie przywiązuję do tego uwagi, który wzór jest pierwszy, a który to drugi. Jak rozwiązujemy równanie kolejność obliczonych pierwiastków nie jest ważna. Stąd w zadaniach bywa, że oznaczyłem \({{x}_{1}}=\frac{-b+\sqrt{\Delta }}{2\cdot a}\) , a \({{x}_{2}}=\frac{-b-\sqrt{\Delta }}{2\cdot a}\)
Jak rozwiązywać równania kwadratowe w zadaniach?
Rozwiąż równanie kwadratowe: \({{x}^{2}}+2x+1=0\)
Rozwiązanie:
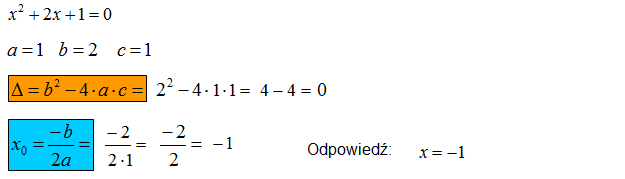
W tym przykładzie delta jest równa zero, więc stosujemy wzór na jeden pierwiastek rzeczywisty.
Zauważamy, że dane równanie kwadratowe można również rozwiązać wykorzystując wzór skróconego mnożenia: \({{a}^{2}}+2ab+{{b}^{2}}={{\left( a+b \right)}^{2}}\) Wówczas otrzymujemy: \[\begin{align} & {{x}^{2}}+2x+1=0 \\ & {{\left( x+1 \right)}^{2}}=0 \\ & x=-1 \\ \end{align}\] Jest to szybka i krótka metoda, ale nie zawsze każdy to zauważy.
Rozwiąż równanie kwadratowe zupełne: \({{x}^{2}}+4x+3=0\)
Rozwiązanie:
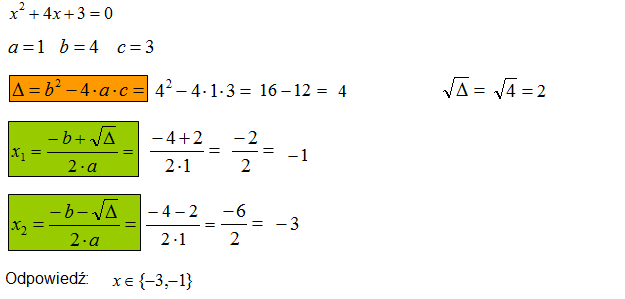
Zwłaszcza na początku nauki o równaniach kwadratowych warto wypisać współczynniki trójmianu kwadratowego a, b, c. Dalej wstawiamy współczynniki do tzw. delty, czyli do wyróżnika trójmianu kwadratowego.
Po obliczeniu delty patrzymy na jej znak:
- Δ > 0 masz 2 pierwiastki rzeczywiste
- Δ = 0 masz 1 pierwiastek rzeczywisty
- Δ < 0 brak pierwiastków rzeczywistych
Rozwiąż równanie kwadratowe zupełne: \({{x}^{2}}+3 x-4=0\)
Rozwiązanie:
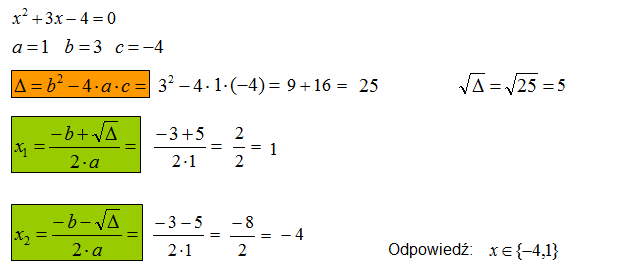
Rozwiąż równanie kwadratowe zupełne: \({{x}^{2}}+6x+8=0\)
Rozwiąż równanie kwadratowe zupełne: \({{x}^{2}}+x-6=0\)
Rozwiąż równanie kwadratowe zupełne: \({{x}^{2}}=-x+2\)
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Rozwiąż równanie kwadratowe zupełne: \({{x}^{2}}-4x+5=0\)
Treść dostępna po opłaceniu abonamentu.Rozwiąż równanie kwadratowe: \(-14x+49=-{{x}^{2}}\)
Treść dostępna po opłaceniu abonamentu.Rozwiąż równanie kwadratowe: \({{x}^{2}}+x+\frac{1}{4}=0\)
Treść dostępna po opłaceniu abonamentu.- Definicja funkcji kwadratowej
- Funkcja kwadratowa – wzory
- Wykres funkcji kwadratowej
- Dziedzina i zbiór wartości funkcji kwadratowej
- Monotoniczność funkcji kwadratowej
- Miejsca zerowe funkcji kwadratowej
- Postać iloczynowa trójmianu kwadratowego
- Równanie kwadratowe
- Równania kwadratowe niezupełne
- Równania sprowadzalne do równań kwadratowych
- Nierówności kwadratowe
- Funkcja kwadratowa – sprawdzian




