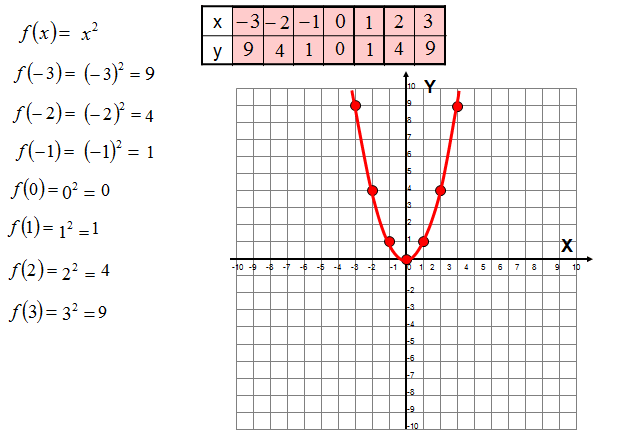
Wykres funkcji kwadratowej

Najprostszy wykres funkcji kwadratowej możesz wykonać, tworząc tabelkę i wyznaczając kilka punktów wykresu.

Wykresem funkcji kwadratowej jest krzywa zwana parabolą.

Aby narysować wykres funkcji kwadratowej najlepiej wyznaczyć miejsca zerowe (o ile istnieją) oraz wierzchołek paraboli i punkt przecięcia paraboli z osią Y.

Przykład:

Dana funkcja: \(y={{-x}^{2}}-x+2\)

W celu naszkicowania wykresu:

1) wyznaczam miejsca zerowe funkcji kwadratowej(o ile istnieją) – punkty przecięcia z osią X. W zadaniach możesz to zrobić na kilka sposobów. W tym uogólnionym przypadku stosujesz wzory na miejsca zerowe funkcji kwadratowej. \[\Delta ={{b}^{2}}-4\cdot a\cdot c={{\left( -1 \right)}^{2}}-4\cdot \left( -1 \right)\cdot 2=1+8=9\] \[{{x}_{1}}=\frac{-b-\sqrt{\Delta }}{2\cdot a}=\frac{-\left( -1 \right)-\sqrt{9}}{2\cdot \left( -1 \right)}=\frac{1-3}{-2}=1\] \[{{x}_{2}}=\frac{-b+\sqrt{\Delta }}{2\cdot a}=\frac{-\left( -1 \right)+\sqrt{9}}{2\cdot \left( -1 \right)}=\frac{1+3}{-2}=-2\]

2) Wyznaczamy wierzchołek paraboli \[W\ \left( p,q \right)\] ,gdzie \[p=\frac{-b}{2a}=\frac{-\left( -1 \right)}{2\cdot \left( -1 \right)}=-\frac{1}{2}\] \[q=\frac{-\Delta }{4a}=\frac{-9}{4\cdot \left( -1 \right)}=\frac{9}{4}=2\frac{1}{4}\]

3) Określam znak współczynnika „a” przy x². Jeśli a > 0 to parabola jest skierowana ramionami do góry. Jeśli a < 0 parabola jest skierowana ramionami do dołu. W naszym przypadku a = -1 więc ramiona skierowane do dołu.

4) Wyznaczam punkt przecięcia paraboli z osią Y wstawiając do wzoru funkcji za x liczbę 0 (x = 0).
Otrzymujemy: \[y=-{{x}^{2}}-x+2=-{{0}^{2}}-0+2=2\] Zatem punkt przecięcia paraboli z osią Y ma współrzędne (0, 2)

5) Zaznaczamy wyznaczone punkty w układzie współrzędnych.

Zauważ, że wierzchołek leży idealnie na wysokości środka odcinka, którego końcami są miejsca zerowe paraboli.

Wykres paraboli – przykład

Wykres funkcji y=x² jest najprostszym wykresem funkcji kwadratowej, której postać ogólna wygląda następująco: y=ax²+bx+c. Krzywą będącą wykresem, nazywa się parabolą. Jej położenie zależy od współczynników a, b i c.

Zadanie.

Naszkicuj wykresy funkcji kwadratowej: y=x².

x

http://www.youtube.com/watch?v=hjEpSjpLOiI

Zobacz na stronie

Zobacz na YouTube