Funkcja kwadratowa – Sprawdzian

Mając funkcję kwadratową: \(y={{x}^{2}}+5x+6\)

1. Wyznacz współczynniki a, b, c
2. Odpowiedz, czy parabola jest skierowana ramionami do góry, czy do dołu
3. Wyznacz deltę i odpowiedz, ile miejsc zerowych ma ta funkcja
4. Wyznacz miejsca zerowe
5. Wyznacz współrzędne wierzchołka paraboli
6. Określ współrzędne przecięcia się paraboli z osiami X i Y
7. Wyznacz wartość funkcji dla argumentu -5
8. Wykonaj wykres tej funkcji
9. Sprawdź, czy punkt (1,3) należy do wykresu funkcji
10. Określ przedziały monotoniczności funkcji kwadratowej
11. Dla jakich argumentów wartości funkcji są większe od zera
12. Dla jakich argumentów wartości funkcji są mniejsze od zera
13. Dla jakich argumentów wartości funkcji są mniejsze od 6
14. Oblicz pole trójkąta, którego wierzchołki tworzą punkty przecięcia się wykresu z osiami X i Y

1) Wyznacz współczynniki a, b, c \[y={{x}^{2}}+5x+6\] a = 1, b = 5, c = 6
Współczynniki a, b, c są bardzo przydatne do obliczania delty.

2) Odpowiedz, czy parabola jest skierowana ramionami do góry, czy do dołu
\(a>0 \) zatem parabola skierowana jest ramionami do góry.

3) Wyznacz deltę i odpowiedz, ile miejsc zerowych ma ta funkcja kwadratowa
\(\Delta ={{b}^{2}}-4\cdot a\cdot c={{5}^{2}}-4\cdot 1\cdot 6=25-24=1\) delta jest dodatnia, więc mamy dwa pierwiastki rzeczywiste.

4) Wyznacz miejsca zerowe
\[{{x}_{1}}=\frac{-b-\sqrt{\Delta }}{2\cdot a}=\frac{-5-1}{2\cdot 1}=\frac{-6}{2}=-3\] \[{{x}_{2}}=\frac{-b+\sqrt{\Delta }}{2\cdot a}=\frac{-5+1}{2\cdot 1}=\frac{-4}{2}=-2\]

5) Wyznacz współrzędne wierzchołka paraboli
\[\begin{align} & a=1,\ b=5,\ c=6 \\ & \Delta =1\ (z\ pkt.3) \\ \end{align}\] \(W\ \left( p,q \right)\) współrzędne wierzchołka paraboli, gdzie \[p=\frac{-b}{2a}=\frac{-5}{2\cdot 1}=-2,5\] \[q=\frac{-\Delta }{4a}=\frac{-1}{4\cdot 1}=-0,25\] \[W\ \left( -2,5\ ;\ -0,25 \right)\]

6) Określ współrzędne przecięcia się paraboli z osiami X i Y
Współrzędne przecięcia z osią X to miejsca zerowe. Wiadomo, że funkcja w miejscu zerowym przyjmuje wartość zero, czyli y = 0. Zatem tutaj nie ma dużo roboty, ponieważ miejsca zerowe zostały wyznaczone w punkcie (4): \({{x}_{1}}=-3,\ {{x}_{2}}=-2\)

Odp.:Współrzędne przecięcia paraboli z osią X: \(\left( -2,0 \right)\ i\ \left( -3,0 \right)\).

Współrzędne przecięcia z osią Y mają zawsze współrzędną x = 0. Zatem do wzoru z niewiadomą x wstawiasz „0”.

\[y={{x}^{2}}+5x+6\] \[y={{0}^{2}}+5\cdot 0+6=6\] Odp.:Współrzędna przecięcia paraboli z osią Y: (0, 6).

7) Wyznacz wartość funkcji dla argumentu -5
Należy w miejsce niewiadomej x wstawić liczbę „-5”. \[y={{\left( -5 \right)}^{2}}+5\cdot \left( -5 \right)+6\] \[y=25-25+6=6\] Odp.: Wartość funkcji dla argumentu -5 wynosi 6. Można to inaczej zapisać: f(-5) = 6.

8) Wykonaj wykres tej funkcji
W tym punkcie bierzemy wybrane informacje obliczone na początku zadania.
Miejsca zerowe: \(\left( -2,0 \right)\ i\ \left( -3,0 \right)\)
Współrzędne wierzchołka paraboli: \(W\ \left( -2,5\ ;\ -0,25 \right)\)
Nie jest to konieczne, ale dobrze również wyznaczyć punkt przecięcia wykresu z osią Y: (0, 6). Teraz rysujesz układ współrzędnych i zaznaczasz charakterystyczne punkty funkcji kwadratowej.

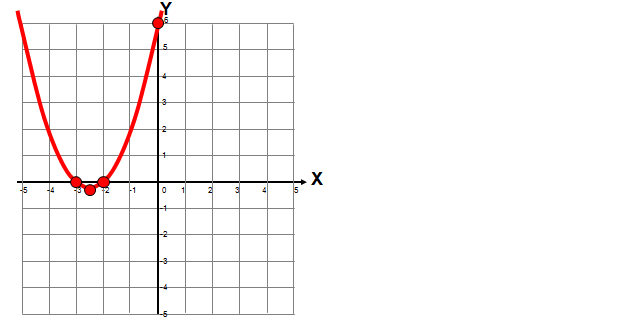
9) Sprawdź, czy punkt (1, 3) należy do wykresu funkcji
Masz wzór funkcji \(y={{x}^{2}}+5x+6\) oraz x = 0, y = 3 ponieważ dany jest punkt o współrzędnych (1, 3). Zatem w miejsce x wstawiasz „0”, a za y wstawiasz „3”. \begin{align} & 3={{1}^{2}}+5\cdot 1+6 \\ & 3=1+5+6 \\ & 3\ne 12 \\ \end{align} Otrzymaliśmy sprzeczność, zatem punkt (1, 3) nie należy do wykresu funkcji kwadratowej.

10) Określ przedziały monotoniczności funkcji kwadratowej
Mam nadzieję, że zauważyłeś, iż parabola jest wykresem funkcji niemonotonicznej (tzw. monotonicznej przedziałami). W zadaniu wykorzystujemy wykres paraboli i współrzędne jej wierzchołka: \(W\ \left( -2,5\ ;\ -0,25 \right)\)
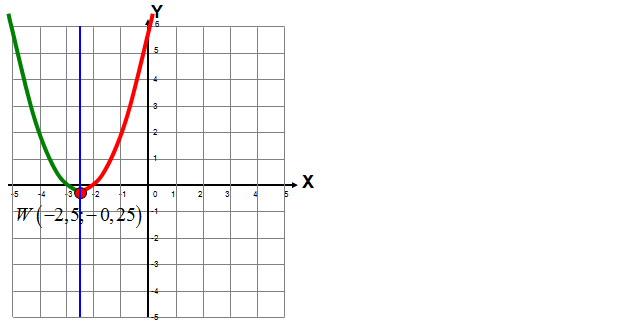Funkcja jest malejąca w przedziale: \(\left( -\infty ; \right.\left. -2,5 \right\rangle \)
Funkcja jest rosnąca w przedziale: \(\left\langle -2,5; \right.\left. +\infty \right)\)

11) Dla jakich argumentów wartości funkcji są większe od zera.
W zadaniu x = ?, zaś y > 0. Zatem graficznie naszym rozwiązaniem są x-sy, których współrzędne y > 0, czyli leżą nad osią X. Wykorzystujemy rysunek paraboli z naszego zadania. 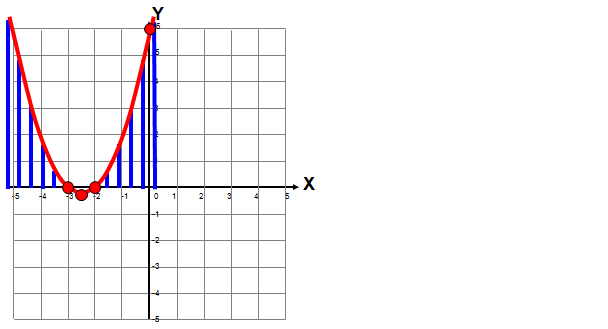Odp.: Dla \(x\in \left( -\infty ,-3 \right)\cup \left( -2,+\infty \right)\)

12) Dla jakich argumentów wartości funkcji są mniejsze od zera
W zadaniu x = ?, zaś y < 0. Wykorzystujemy rysunek z punktu 11). Oczywiście tym razem należy zakreskować część wykresu znajdującą się pod osią X, ponieważ tylko tam istnieją współrzędne y < 0.
Odp.: Dla \(x\in \left( -3,-2 \right)\)

13) Dla jakich argumentów wartości funkcji są mniejsze od 6
\[x=?,\quad y<6\] \[\begin{align} & y={{x}^{2}}+5x+6 \\ & {{x}^{2}}+5x+6<6 \\ & {{x}^{2}}+5x<0 \\ & x\left( x+5 \right)<0 \\ & {{x}_{1}}=0\quad {{x}_{2}}=-5 \\ \end{align}\] Odp.: Dla \(x\in \left( -5,0 \right)\)

14) Oblicz pole trójkąta, którego wierzchołki tworzą punkty przecięcia się wykresu z osiami X i Y
Korzystając z wykresu odczytujemy długość podstawy, którą jest odległość między miejscami zerowymi. Odczytujemy również wysokość trójkąta rozwartokątnego. 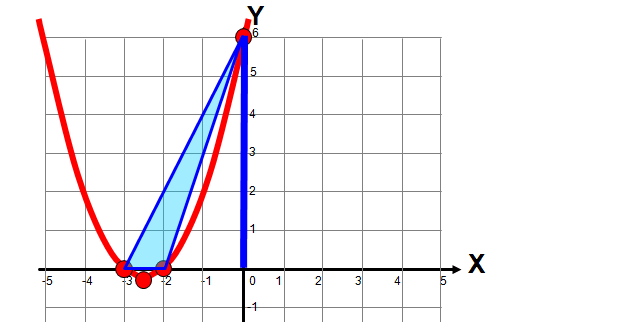\[P=\frac{a\cdot h}{2}=\frac{1\cdot 6}{2}=3\] Odp.: Pole trójkąta wynosi 3 jednostki kwadratowe.

Mając funkcję kwadratową \(y=-{{x}^{2}}+x+6\)

1. Wyznacz współczynniki a, b, c
2. Odpowiedz, czy parabola jest skierowana ramionami do góry, czy do dołu
3. Wyznacz deltę i odpowiedz ile miejsc zerowych ma ta funkcja
4. Wyznacz miejsca zerowe funkcji
5. Wyznacz współrzędne wierzchołków paraboli
6. Określ współrzędne punktów przecięcia się paraboli z osiami X i Y
7. Wyznacz wartość funkcji dla argumentu \(-\frac{1}{10}\)
8. Wykonaj wykres funkcji
9. Sprawdź, czy punkt P (-1, 4) należy do wykresu funkcji
10. Określ przedziały monotoniczności funkcji kwadratowej
11. Dla jakich argumentów wartości funkcji są większe od zera
12. Dla jakich argumentów wartości funkcji są mniejsze od zera
13. Dla jakich argumentów wartości funkcji są nie większe od 4
14. Wyznacz współrzędne punktów przecięcia się danej funkcji kwadratowej \(y=-{{x}^{2}}+x+6\) z funkcją liniową \(y=-x+5\)

Mając wzór funkcji \(y=-{{x}^{2}}+8 x-12\)

1. Podaj dziedzinę funkcji
2. Podaj miejsca zerowe funkcji (jeśli istnieją)
3. Wyznacz wierzchołek paraboli
4. Podaj współrzędne punktów przecięcia się wykresu z osią X i Y
5. Wykonaj wykres funkcji
6. Podaj najmniejszą i największa wartość funkcji (jeśli istnieje)
7. Podaj zbiór wartości funkcji
8. Wyznacz przedziały monotoniczności
9. Dla jakich argumentów funkcja przyjmuje wartości mniejsze od -8