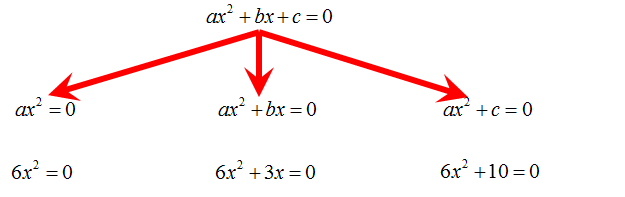Równania kwadratowe niezupełne
Postać ogólna funkcji kwadratowej to \(y=a{{x}^{2}}+bx+c\). Równanie kwadratowe jest niezupełne, gdy składa się dwóch lub jednego jednomianu. Współczynniki b lub c są równe zero.
Równania kwadratowe niezupełne stanowią ważną część wiedzy o funkcji kwadratowej. Musisz wiedzieć, że omawiane równania są stosunkowo łatwe do obliczania w porównaniu z innymi zagadnieniami tego działu matematycznego.
Równanie kwadratowe niezupełne można rozwiązywać przy pomocy:
- wyróżnika kwadratowego (tzw. delty), lecz istnieją znacznie prostsze metody wyznaczania pierwiastków tych równań
- rozkładu na czynniki – wówczas rozwiązanie takiego równania będzie dość łatwe i krótkie
Podział równań kwadratowych niezupełnych
Równania kwadratowe niezupełne – zadania
Rozwiąż równanie kwadratowe niezupełne: \(4{{x}^{2}}=8\)
Rozwiązanie: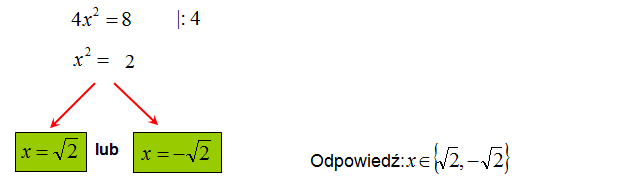
Rozwiąż równanie kwadratowe niezupełne: \(6{{x}^{2}}+2x=0\)
Rozwiązanie:
Najczęściej takie równania rozwiązujemy przez wyłączenie niewiadomej x przed nawias. Otrzymujemy wówczas dwa czynniki, które równają się 0. Pierwszy czynnik to wyłączony x, drugi czynnik to nawias.
W takim przypadku przyrównujemy dwa nawiasy do zera. Dlaczego? Jeśli iloczyn jest równy zero, to pierwszy czynnik musi być zerem lub drugi czynnik musi być równy zero.
Rozwiąż równanie kwadratowe niezupełne: \(8{{x}^{2}}=5x\)
Rozwiąż równanie kwadratowe niezupełne: \(\frac{1}{3}x-\frac{6}{7}{{x}^{2}}=0\)
W równaniach kwadratowych niezupełnych w których występują mianowniki warto na początku usunąć właśnie mianowniki. W tym celu mnożymy równanie przez wspólny mianownik występujących mianowników.
Rozwiąż równanie kwadratowe niezupełne: \(\frac{4}{5}x=\frac{1}{10}{{x}^{2}}\)
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Rozwiąż równanie kwadratowe niezupełne: \(8{{x}^{2}}-4=0\)
Treść dostępna po opłaceniu abonamentu.Rozwiąż równanie kwadratowe niezupełne: \({{x}^{2}}+4=0\)
Treść dostępna po opłaceniu abonamentu.Rozwiąż równanie kwadratowe niezupełne: \(25{{x}^{2}}-4=0\)
Treść dostępna po opłaceniu abonamentu.- Definicja funkcji kwadratowej
- Funkcja kwadratowa – wzory
- Wykres funkcji kwadratowej
- Dziedzina i zbiór wartości funkcji kwadratowej
- Monotoniczność funkcji kwadratowej
- Miejsca zerowe funkcji kwadratowej
- Postać iloczynowa trójmianu kwadratowego
- Równanie kwadratowe
- Równania kwadratowe niezupełne
- Równania sprowadzalne do równań kwadratowych
- Nierówności kwadratowe
- Funkcja kwadratowa – sprawdzian