Miejsca zerowe funkcji kwadratowej

1) Jeśli masz postać ogólną funkcji kwadratowej: \(y=a{{x}^{2}}+bx+c\) najczęściej miejsca zerowe oblicza się przez wyznaczenie współczynników a,b,c przy kolejnych potęgach x.

2) Znając wzór na wyróżnik trójmianu kwadratowego (wzór na deltę) \[\Delta ={{b}^{2}}-4\cdot a\cdot c\] obliczasz wartość delty, a następnie wybierasz jedną z trzech możliwości:

• jeśli Δ > 0 wówczas mamy dwa miejsca zerowe: \[{{x}_{1}}=\frac{-b-\sqrt{\Delta }}{2\cdot a}\] \[{{x}_{2}}=\frac{-b+\sqrt{\Delta }}{2\cdot a}\]
• jeśli Δ = 0 wówczas mamy jedno miejsce zerowe o wzorze: \[{{x}_{0}}=\frac{-b}{2\cdot a}\]
• jeśli Δ < 0 to brak miejsc zerowych

Przykład.

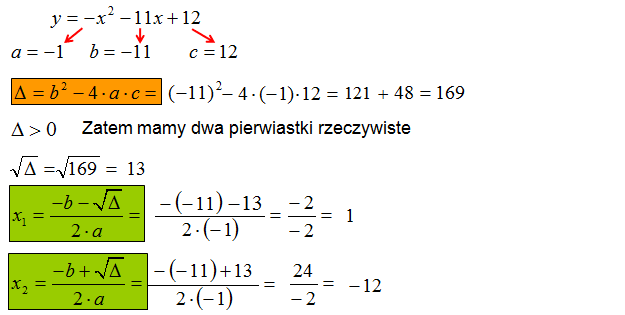
Wyznacz miejsca zerowe funkcji kwadratowej \(y=-{{x}^{2}}-11x+12\)

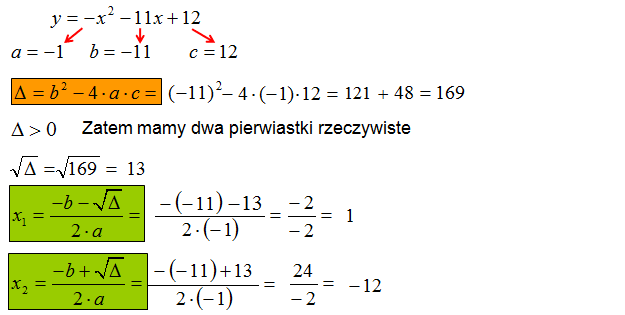
Odpowiedź: Miejsca zerowe tej funkcji kwadratowej to 1 i -12.

Zobacz, jak rozwiązywać równania kwadratowe? Jest to zagadnienie ściśle związane z obliczaniem miejsc zerowych trójmianu kwadratowego.