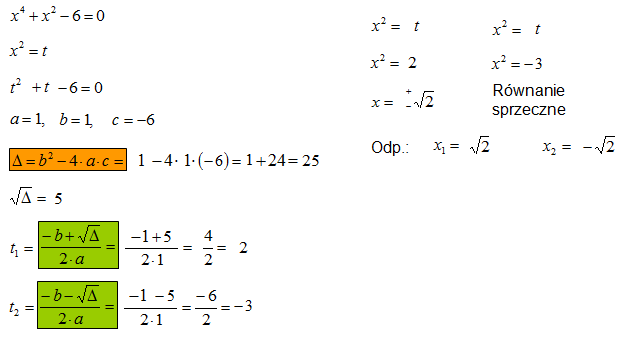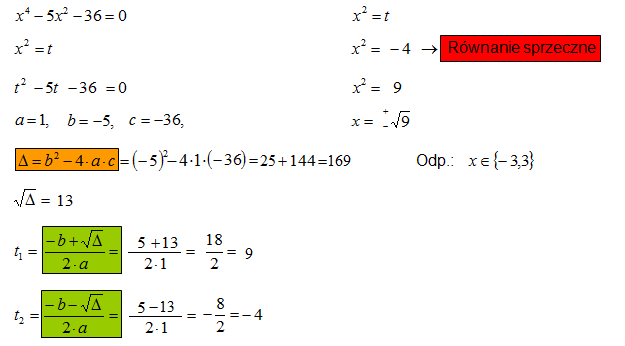Równania sprowadzalne do równań kwadratowych – Przykłady i zadania

Równania sprowadzalne do równań kwadratowych rozwiązuje się przez podstawienie do równania w miejsce x² literki np. „t”. Takie działanie obniża stopień równania, sprowadzając je zarazem do równania kwadratowego (stopnia drugiego).

Równania prowadzące do równań kwadratowych w zadaniach

Zadanie.

Rozwiąż równanie: \({{x}^{4}}+{{x}^{2}}-6=0\)

Równanie sprowadzone do równania kwadratowego

https://www.youtube.com/watch?v=Xp8jqfcJU_c

Zobacz na stronie

Zobacz na YouTube

Rozwiązanie równania sprowadzalnego do równania kwadratowego

Krok 1.
Wykonujesz podstawienie, najczęściej jest to x² = t. W tym miejscu zauważasz, że x⁴ = (x²)² widzisz więc, że wnętrze nawiasu możesz zastąpić literką „t” zgodnie z podstawieniem. Zatem x⁴ = (x²)² = (t)². Tym to sposobem obniżasz stopień równania do równania kwadratowego.

Krok 2.
Obliczasz równanie kwadratowe z niewiadomą „t”. Wiadomo, wyznaczasz współczynniki a, b, c począwszy od najwyższego stopnia równania kwadratowego. Wyznaczasz deltę (wyróżnik równania kwadratowego).
Jeśli:

Δ > 0 wówczas mamy dwa pierwiastki rzeczywiste
Δ = 0 jest jeden pierwiastek rzeczywisty
Δ < 0 wówczas nie ma pierwiastków równanie kwadratowe

Rozwiązaniem równania kwadratowego w zależności od znaku delty może być jedno, dwa lub brak rozwiązań.

Przy delcie dodatniej uzyskujesz dwa pierwiastki równania z niewiadomą t. W tym kroku po prostu uzyskujesz wartość niewiadomej t. Czyli t₁ = liczba1, t₂ = liczba2.

Krok 3.
Obliczasz wartość niewiadomej x korzystając z podstawienia x² = t. W miejsce literki „t” wstawiasz jej wartości liczbowe obliczone w kroku 2. W zależności od ilości pierwiastków „t”, wstawiasz jedną lub dwie liczby w miejsce literki „t”. Dalej obliczasz proste jedno lub dwa równania kwadratowe z niewiadomą x.

Zadanie.

Rozwiąż równanie: \({{x}^{4}}-5{{x}^{2}}-36=0\)