Dziedzina i zbiór wartości funkcji kwadratowej

Zauważ, że dziedziną funkcji kwadratowej jest zbiór wszystkich liczb rzeczywistych: \(D\in R\)
Do wzoru funkcji kwadratowej możesz wstawiać wszystkie liczby rzeczywiste. Nie ma żadnych zakazów.

Zbiorem wartości funkcji kwadratowej jest przedział, którego wyznaczenie zaczyna się od wyznaczenia współrzędnych wierzchołka paraboli, a w zasadzie współrzędnej y wierzchołka paraboli.

Przypomnij sobie pojęcie dziedziny i zbioru wartości funkcji.

Przykład.
Zbiór wartości funkcji: \(y={{x}^{2}}-4x+8\) wyznaczamy, zaczynając od obliczenia współrzędnej y wierzchołka paraboli:
\[W\ \left( p,q \right)\] Oczywiście najpierw obliczymy deltę: \[\Delta ={{b}^{2}}-4\cdot a\cdot c={{\left( -4 \right)}^{2}}-4\cdot 1\cdot 8=16-32=-16\] Teraz współrzędne wierzchołka paraboli: \[p=\frac{-\left( -4 \right)}{2\cdot 1}=2\] \[q=\frac{-\Delta }{4a}=\frac{-\left( -16 \right)}{4\cdot 1}=4\] Wiemy, że ramiona są skierowane do góry, ponieważ współczynnik przy x² jest dodatni, druga współrzędna wierzchołka paraboli, to y = 4. Zatem zbiorem wartości tej funkcji kwadratowej jest przedział: \[Y=\left\langle 4,\left. +\infty \right) \right.\] W zasadzie nie trzeba wykonywać wykresu funkcji kwadratowej, lecz w ramach wytłumaczenia zerknij na rysunek.

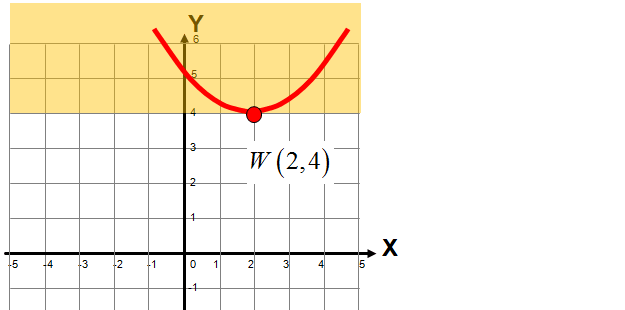
Wyznacz dziedzinę i zbiór wartości funkcji kwadratowej

Zadanie.

Wyznacz na podstawie wykresu dziedzinę funkcji kwadratowej: y=x².

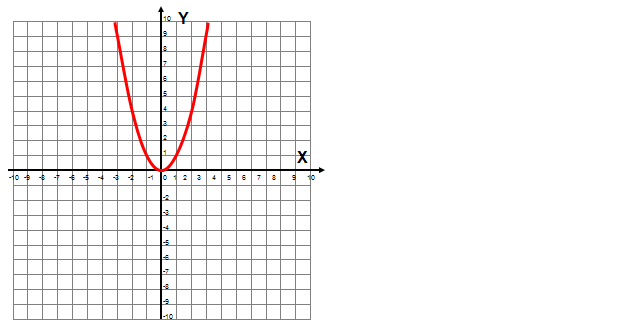
Rozwiązanie – dziedzina funkcji kwadratowej:

x

https://www.youtube.com/watch?v=f66A1n_yxes

Zobacz na stronie

Zobacz na YouTube