Monotoniczność funkcji
Definicja monotoniczności funkcji:
- Funkcja f jest rosnąca (silnie rosnąca) jeśli
dla każdego \({{x}_{1}}<{{x}_{2}}\) prawdziwy jest warunek \(f\left( {{x}_{1}} \right)<f\left( {{x}_{2}} \right)\) - Funkcja f jest malejąca (silnie malejąca) jeśli
dla każdego \({{x}_{1}}<{{x}_{2}}\) prawdziwy jest warunek \(f\left( {{x}_{1}} \right)>f\left( {{x}_{2}} \right)\) - Funkcja f jest stała jeśli
dla każdego \({{x}_{1}}<{{x}_{2}}\) prawdziwy jest warunek \(f\left( {{x}_{1}} \right)=f\left( {{x}_{2}} \right)\)
- Funkcja f jest niemalejąca (słabo rosnąca) jeśli
dla każdego \({{x}_{1}}<{{x}_{2}}\) prawdziwy jest warunek \(f\left( {{x}_{1}} \right)\le f\left( {{x}_{2}} \right)\) - Funkcja f jest nierosnąca (słabo malejąca) jeśli
dla każdego \({{x}_{1}}<{{x}_{2}}\) prawdziwy jest warunek \(f\left( {{x}_{1}} \right)\ge f\left( {{x}_{2}} \right)\)

Monotoniczność funkcji z wykresu
Zbadaj monotoniczność funkcji z wykresu. Wówczas możesz wyobrazić sobie, że „funkcja jest wzgórzem”, po którym wspina się człowiek. Podczas takiego podejścia wykres czytamy od lewej do prawej strony. „Ludzik” wędrujący po wykresie również musi się przemieszczać od lewej do prawej strony funkcji.
Podczas takiego określania monotoniczności funkcji jeśli ludzik w pewnym przedziale wspina się ku górze to mówimy, że funkcja jest rosnąca. W przypadku, gdy schodzi na dół to mówimy, że jest malejąca. Gdy zaś idzie po linii poziomej mówimy, że w tym przedziale funkcja jest stała.
Zbadaj monotoniczność funkcji (tzn. określ, czy funkcja jest rosnąca, malejąca, czy stała).
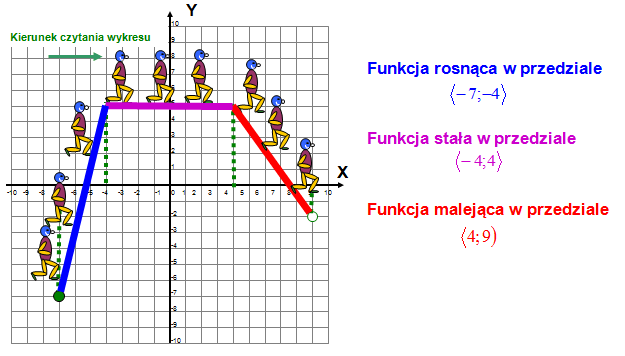
Uwaga: Podana wyżej funkcja nie jest monotoniczna, ponieważ w niektórych przedziałach jest rosnąca w innych malejąca. Funkcja jest monotoniczna jeśli w całej dziedzinie jest nierosnąca (malejąca lub stała) lub niemalejąca (rosnąca lub stała). Podana wyżej funkcja jest monotoniczna przedziałami.
Problem z nawiasami na końcach przedziałów monotoniczności
Niekiedy w literaturze możesz spotkać nawiasy domknięte jak i otwarte na końcach przedziałów monotoniczności.
Warto tutaj jednak powiedzieć, że nie bada się monotoniczności funkcji w punkcie.
Jeśli jesteś maturzystą podczas badania monotoniczności funkcji należy domykać przedziały.
Sposób udzielania odpowiedzi
Ważnym aspektem monotoniczności funkcji jest także udzielanie odpowiedzi. Nie wolno używać sformułowania: „Funkcja jest rosnąca dla x∈<0,+∞)”. Taki zapis dopuszcza domyślnie monotoniczność funkcji w jednym punkcie np. w x = 5, a wiemy, że monotoniczność jest rozpatrywana na przedziałach lub miedzy dwoma punktami. Prawidłowy zapis brzmi: „Funkcja jest rosnąca w przedziale <0,+∞)”.

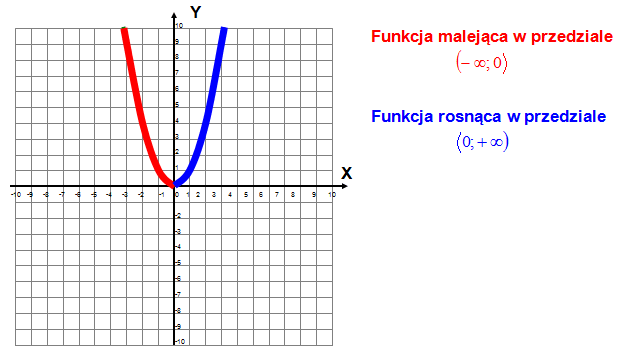
Monotoniczność, a funkcja kwadratowa
Spójrz na definicję monotoniczności funkcji. Żaden ze wzorów nie pasuje do funkcji kwadratowej. Nasza funkcja nie jest rosnąca, malejąca, ani stała.
Mamy tu przykład funkcji niemonotonicznej albo inaczej monotonicznej przedziałami.
Nasza funkcja w całej dziedzinie nie spełnia warunków określających monotoniczność funkcji. Zauważ, że jeśli będziemy funkcję rozpatrywać tylko w określonych przedziałach to w tychże przedziałach będzie już monotoniczna i będzie spełniała warunki określające monotoniczność funkcji.
Zbadaj monotoniczność funkcji (tzn. określ, czy funkcja jest rosnąca, malejąca, czy stała) y=x2.