Naszkicuj i narysuj wykresy funkcji
- Ogólne wskazówki jak naszkicować i narysować wykresy funkcji
- Wykres funkcji określonej słownie
- Wykres funkcji liniowej
- Wykres funkcji liniowej stałej
- Wykres funkcji z wartością bezwzględną, z modułem
- Wykres funkcji kwadratowej – parabola
- Hiperbola – wykres funkcji wymiernej
- Wykres funkcji określonej na przedziałach
Ogólne wskazówki jak naszkicować i narysować wykresy funkcji
Proszę, narysuj wykres funkcji.
Nie ma sprawy choć wolałbym, abyś sam to uczynił już teraz online. Ja tylko dam Ci najważniejsze wskazówki dotyczące rysowania prostych wykresów funkcji. Oto one:
Na początku zastanów się, jakie liczby należą do dziedziny, a jakie nie, czyli jakie liczby możesz wstawić do wzoru funkcji. Musisz uważać, aby do mianownika nie wstawić liczby, która go zeruje lub jeśli masz pierwiastek to uważaj, aby liczba stojąca pod znakiem pierwiastka nie była ujemna. Zwracasz także uwagę na słowne ograniczenia lub podaną jawnie dziedzinę w treści zadania.
Teraz możesz narysować tabelkę i w górnym wierszu wstawiasz kilka liczb z dziedziny funkcji. Niekiedy uczniowie pytają jakie liczby z dziedziny można wstawić do tabelki. Przy prostych funkcjach jak funkcja liniowa do tabelki najlepiej wstawić te liczby, które są całkowite i leżą blisko początku układu współrzędnych. Będziesz chciał ten wykres narysować zazwyczaj blisko początku układu współrzędnych.
Po wstawieniu kilku liczb z dziedziny do tabelki możesz wyznaczyć na podstawie wzoru wartość funkcji.
Gdy już wykonasz tabelkę zauważasz, że każda kolumna jest punktem o określonych współrzędnych.
Zaznaczasz zatem współrzędne punktów w układzie współrzędnych. Dalej musisz się zastanowić czy możesz te punkty połączyć prostą lub krzywą. Zwykle informują nas o tym dodatkowe informacje w zadaniu lub też podana lub wyznaczona dziedzina funkcji.
Zazwyczaj należy połączyć punkty otrzymując narysowany wykres funkcji.
Wykres funkcji określonej słownie
Narysuj wykres funkcji określonej następująco: „Każdej liczbie naturalnej mniejszej niż 4 przyporządkuj jej trzykrotność”.
Rozwiązanie
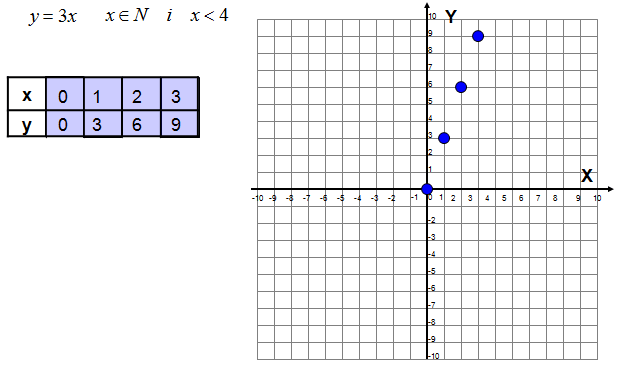
Ważnym szczegółem w tym zadaniu dotyczącym rysowania wykresów jest fakt, że punktów w tym przypadku nie łączymy. Wynika to z faktu, że funkcja jest określona nie dla wszystkich liczb rzeczywistych tylko dla liczb naturalnych.
Teraz zobacz kilka innych przykładów typu: jak narysować, naszkicować wykres funkcji online?
Wykres funkcji liniowej
Chcąc naszkicować wykres funkcji liniowej należy wykonać tabelkę z wierszami x i y. W kolejnym kroku wstaw do niej minimum dwa argumenty – dwie liczby i oblicz wartości funkcji podstawiając wybrane liczby do wzoru funkcji.
Na końcu łączysz otrzymane punkty prostą. Jeśli punkty nie leżą w jednej prostej, sprawdź swoje rachunki dzięki którym uzupełniłeś tabelkę. Prawdopodobnie powstał błąd. Jeśli jest wszystko dobrze to prosta przetnie wszystkie otrzymane punkty.
Omówienie pojęcia: Wykres funkcji liniowej
Wykres funkcji liniowej stałej
Podczas rysowania wykresu funkcji stałej należy zauważyć, że do tabelki do górnego wiersza można wstawić dowolną liczbę rzeczywistą. W dolnym wierszu należy wstawić tę samą wartość funkcji w naszym przypadku, to liczba „4”. Wykresem funkcji stałej jest prosta równoległa do poziomej osi X.
Omówienie pojęcia: Wykres funkcji liniowej stałej
Wykres funkcji z wartością bezwzględną, z modułem
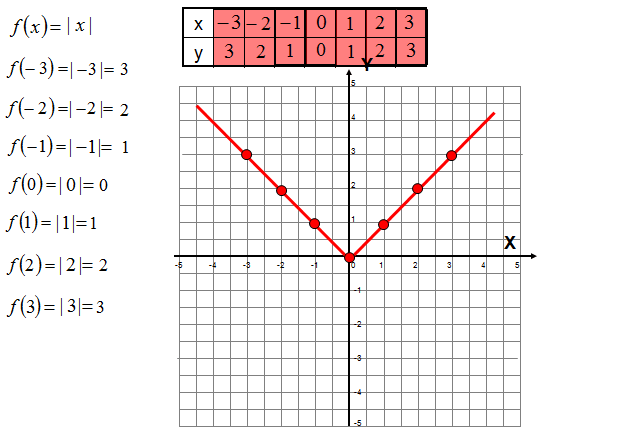
Chciałbym Ci opowiedzieć w jak fascynujący sposób powstaje wykres funkcji z modułem, czyli z wartością bezwzględną. Oczywiście możesz zrobić tabelkę i na podstawie wyznaczonych punktów naszkicować wykres funkcji. Ale jest jeszcze inny ciekawy sposób. Omówię go na podstawie funkcji y=|x|.
Na początku narysuj wykres funkcji bez wartości bezwzględnej. W tym wypadku y=x. Jest to bardzo prosta funkcja liniowa. Następnie tę część wykresu, która znajduje się pod poziomą osią X odbijesz symetrycznie nad osią X. Wykres znajdujący się pod osią X wycierasz zostawiając wyłącznie łamaną w dodatniej części osi Y.
W podobny sposób możesz rysować wykresy funkcji z wartością bezwzględną |f(x)| jeśli potrafisz narysować wykres bez wartości bezwzględnej f(x).
Sporządź wykres funkcji z wartością bezwzględną: y=|x|.
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Wykres funkcji kwadratowej – parabola
Wykres funkcji y=x2 jest najprostszym wykresem funkcji kwadratowej, której postać ogólna wygląda następująco: y=ax2+bx+c. Krzywą będącą wykresem, nazywa się parabolą. Jej położenie zależy od współczynników a, b i c.
Omówienie pojęcia: Wykres funkcji kwadratowej
Hiperbola – wykres funkcji wymiernej
Wykres funkcji \(f\left( x \right)=\frac{1}{x}\) jest najprostszym przykładem funkcji wymiernej. Warto tutaj wspomnieć, że wykresem jest krzywa zwana hiperbolą.
Hiperbolę rysujemy najpierw od zaznaczenia dwóch asymptot, czyli linii nie wchodzących w skład wykresu, ale pomagających go narysować. W przypadku poniżej asymptotami są osie X i Y. Hiperbola zbliża się coraz bardziej do asymptot (tutaj osi X i Y), ale nigdy ich nie osiągnie, nie dotknie.
Dana jest funkcja: \(f\left( x \right)=\frac{1}{x}\) w zbiorze \(R – \left\{ 0 \right\}\), wykonaj jej wykres.
Treść dostępna po opłaceniu abonamentu.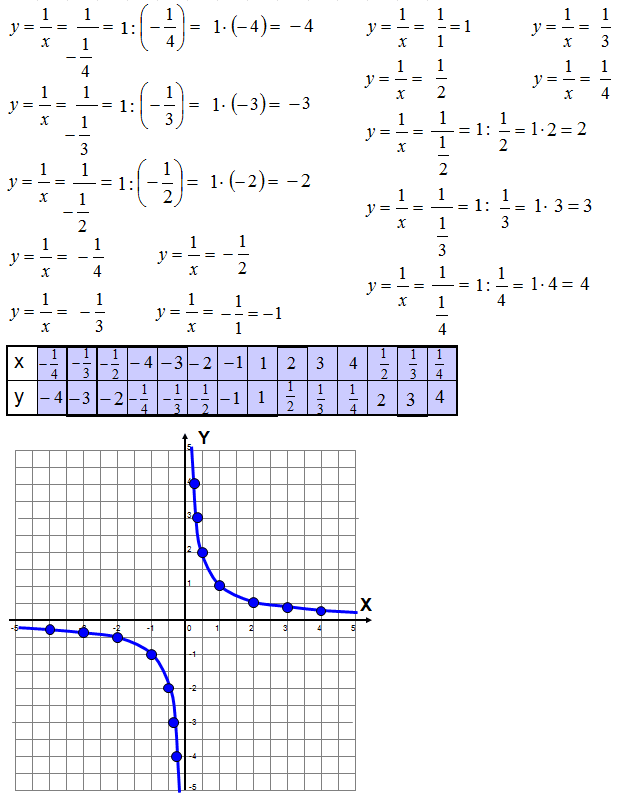
Wykres funkcji określonej na przedziałach
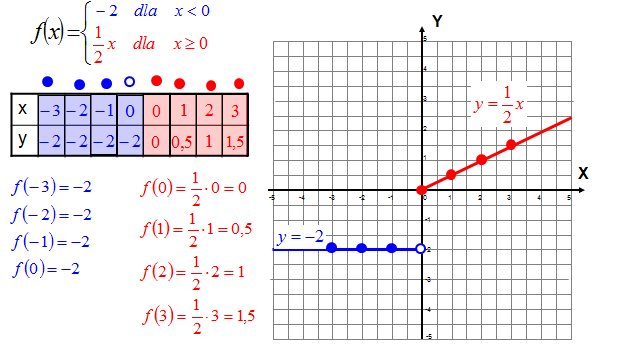
Mając wzór funkcji określonej na przedziałach patrzysz najpierw na przedziały, w których funkcja jest określona. Zazwyczaj daną funkcję w takim przypadku nie rysujesz w całym zbiorze liczb rzeczywistych tylko w podanym przedziale.
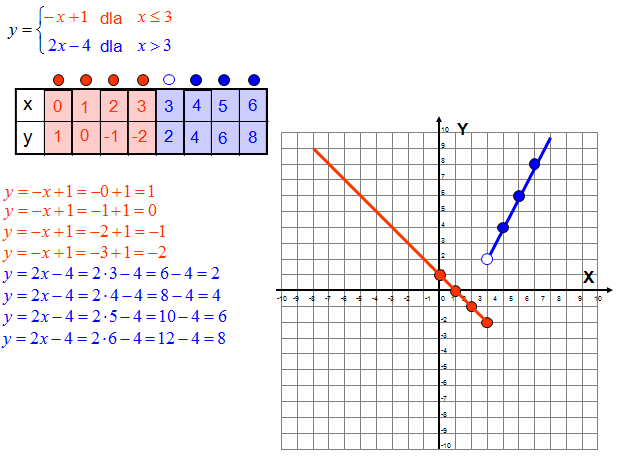
Narysuj wykres funkcji określonej na przedziałach: \[y=\left\{ \begin{matrix} -x+1\quad dla\quad x\le 3 \\ 2x-4\quad dla\quad x>3 \\ \end{matrix} \right.\]
Treść dostępna po opłaceniu abonamentu.