Egzamin gimnazjalny z matematyki 2006 online
Aby przygotować suchą zaprawę do tynkowania ścian, należy zmieszać piasek, wapno i cement odpowiednio w stosunku 15 : 4 : 1. W którym wierszu tabeli podane są właściwe ilości składników potrzebnych do otrzymania 140 kg takiej zaprawy?
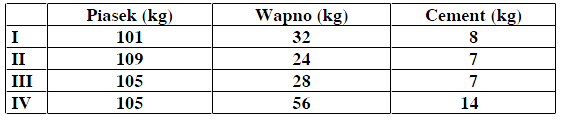
A. I B. II C. III D. IV
Na trójkątnym trawniku zamontowano obrotowy zraszacz. Aby podlać jak największą powierzchnię trawnika, nie oblewając jednocześnie ścieżek, naleśy ustawić zraszacz w punkcie przecięcia
A. środkowych trójkąta.
B. symetralnych boków trójkąta.
C. wysokości trójkąta.
D. dwusiecznych kątów trójkąta.
Trzy lata temu posadzono przed domem krzew. Co roku podwajał on swoją wysokość i teraz ma 144 cm. Jeśli przez x oznaczymy wysokość krzewu w dniu posadzenia, to informacjom z zadania odpowiada równanie
A. x = 144 B. 4x = 144 C. 6x = 144 D. 8x = 144
Informacje do zadań 17. – 20.
Przez 3 godziny Jacek z Magdą obserwowali ruch samochodowy na moście. Liczyli przejeżdżające pojazdy. Wyniki zapisali w tabeli.

Który diagram przedstawia procentowy rozkład liczb pojazdów poszczególnych typów przejeżdżających przez most między 700 a 800?
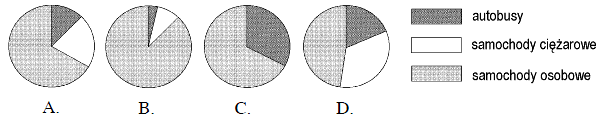
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Które zdanie wynika z danych w tabeli?
A. Między 1000 a 1100 przejedzie przez most jeden autobus.
B. Samochody osobowe jeżdżą szybciej niż samochody ciężarowe.
C. Między 700 a 800 przejechało więcej samochodów osobowych niż pozostałych pojazdów.
D. W ciągu doby przejedzie 8 razy więcej pojazdów niż przejechało między 700 a 1000.
Ile procent liczby wszystkich pojazdów, które przejechały przez most między 700 a 1000, stanowi liczba samochodów osobowych?
A. 68% B. 17% C. 20% D. 12%
Treść dostępna po opłaceniu abonamentu.Ile samochodów osobowych przejeżdżało średnio przez most w ciągu jednej godziny obserwacji?
A. 52/3 B. 6 C. 6 1/3 D. 7
Treść dostępna po opłaceniu abonamentu.Informacje do zadań 21. – 23.
Wykres ilustruje zmiany temperatury gleby w pewnej miejscowości na głębokości 10 cm i 30 cm w ciągu doby w okresie lata.
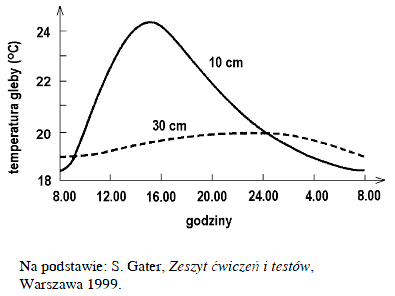
Z analizy wykresu wynika, że
A. w ciągu całej doby temperatura gleby jest niższa na głębokości 30 cm niż na głębokości 10 cm.
B. na obu głębokościach gleba ma najniższą temperaturę o północy.
C. gleba na głębokości 30 cm nagrzewa się wolniej i stygnie wolniej niż glebana głębokości 10 cm.
D. amplituda dobowa temperatur gleby na głębokości 10 cm jest mniejsza niż amplituda dobowa temperatur na głębokości 30 cm.
Jaką temperaturę ma gleba w południe na głębokości 10 cm?
A. Niższą niż 21ºC.
B. Między 22ºC a 23ºC.
C. Między 23ºC a 24ºC.
D. Wyższą niż 24ºC.
Gleba na głębokości 10 cm ma najwyższą temperaturę około godziny
A. 1100 B. 1300 C. 1500 D. 1700
Treść dostępna po opłaceniu abonamentu.Informacje do zadania 28.
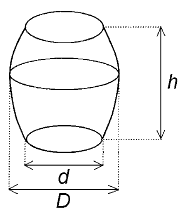
Objętość beczki oblicza się wg wzoru: V =1/12· π · (2D2 + d2) · h, gdzie D – średnica w miejscu najszerszym, d – średnica dna, h – wysokość beczki.
Wojtek obmierzył beczkę w ogrodzie. Ma ona wysokość 12 dm i średnicę dna równą 7 dm. Z powodu trudności ze zmierzeniem średnicy w najszerszym miejscu Wojtek zmierzył obwód w najszerszym miejscu. Jest on równy 33 dm. Oblicz objętość beczki. Dla ułatwienia obliczeń przyjmij π =22/7. Zapisz obliczenia.
 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Wilgotnością drewna nazywamy stosunek masy wody zawartej w drewnie do masy drewna całkowicie suchego. Przyjęto podawać wilgotność drewna w procentach. Ich liczbę (w) obliczamy za pomocą wzoru:
, gdzie M oznacza masę drewna wilgotnego, a m – masę drewna całkowicie suchego. Wyznacz M w zależności od m i w. Zapisz kolejne przekształcenia wzoru.
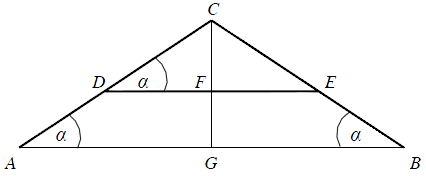
Treść dostępna po opłaceniu abonamentu.Rysunek przedstawia szkic przekroju dachu dwuspadowego. Wysokość dachu GC = 5,4 m, a szerokość podstawy AB = 14,4 m. Oblicz długość krokwi AC i długość belki DE, wiedząc, że odległość belki od podstawy dachu jest równa 2,4 m (czyli FG = 2,4 m). Zapisz obliczenia.
 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Uzupełnij rachunek wystawiony przez firmę budowlaną, wpisując w wykropkowanych miejscach obliczone wartości.

Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.- Egzamin gimnazjalny z matematyki 2017
- Egzamin gimnazjalny z matematyki 2016
- Egzamin gimnazjalny z matematyki 2015
- Egzamin gimnazjalny z matematyki 2014
- Egzamin gimnazjalny z matematyki 2013
- Egzamin gimnazjalny z matematyki 2012
- Egzamin gimnazjalny z matematyki 2011
- Egzamin gimnazjalny z matematyki 2010
- Egzamin gimnazjalny z matematyki 2009
- Egzamin gimnazjalny z matematyki 2008
- Egzamin gimnazjalny z matematyki 2007
- Egzamin gimnazjalny z matematyki 2006
- Egzamin gimnazjalny z matematyki 2005
- Egzamin gimnazjalny z matematyki 2004
- Egzamin gimnazjalny z matematyki 2003
- Egzamin gimnazjalny z matematyki 2002




