Monotoniczność funkcji liniowej
Monotoniczność funkcji liniowej można określić zarówno z danego wykresu, jak i ze wzoru funkcji liniowej. Przeprowadźmy rozważanie na temat monotoniczności funkcji liniowej, dlatego przypomnij sobie co to jest monotoniczność funkcji w sensie ogólnym?
Monotoniczność funkcji liniowej z wykresu określamy, czytając wykres od lewej do prawej.
- Jeżeli wykres wznosi się to funkcja jest rosnąca
- Jeżeli wykres opada to funkcja jest malejąca
- Jeżeli wykres jest równoległy do osi X wówczas funkcja liniowa jest stała
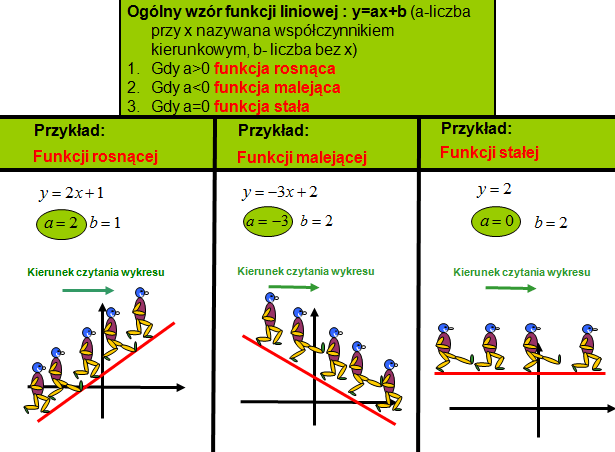
Podczas takiego podejścia możesz sobie wyobrazić, ze „ludzik” idzie po funkcji liniowej. „Ludzika” ustawiasz z lewej strony wykresu, ponieważ czytamy wykres od lewej do prawej. Jeśli „ludzik” wspina się po wykresie to funkcja jest rosnąca, jeśli schodzi na dół to malejąca, jeżeli idzie po linii poziomej to dana funkcja liniowa jest stała.
Monotoniczność funkcji liniowej na podstawie wzoru funkcji.
Mając wzór funkcji liniowej w postaci kierunkowej: y = ax + b zwracasz szczególną uwagę na współczynnik kierunkowy „a”.
- Jeśli a > 0 to funkcja liniowa jest rosnąca
- Jeśli a < 0 to funkcja liniowa jest malejąca
- Jeśli a = 0 to funkcja liniowa jest stała
Zadania z monotoniczności funkcji liniowej są oparte w większości na określeniu znaku współczynnika kierunkowego stojącego przy x we wzorze y = ax + b. Monotoniczność jest jedną z własności funkcji liniowej, dlatego już za chwilę dowiesz się kiedy funkcja jest rosnąca, malejąca i stała? Przekonasz się jak wielką wagę w tego typu zadaniach ma znak współczynnika kierunkowego.
Warunki monotoniczności funkcji liniowej – zadania
W zielonej ramce masz warunki określające monotoniczność funkcji liniowej.
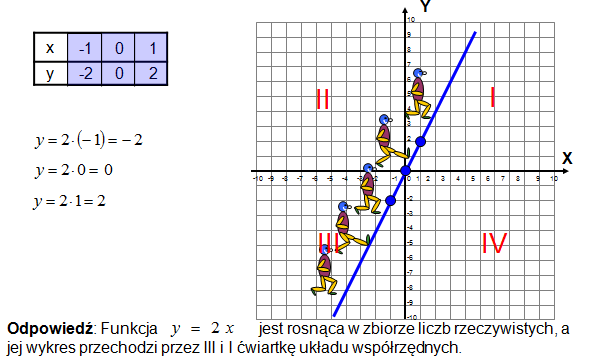
Mając funkcję y = 2x w zbiorze liczb rzeczywistych odpowiedz:
– czy jest to funkcja: rosnąca, malejąca, czy stała?
– przez które ćwiartki układu współrzędnych przechodzi ta funkcja?

Mając funkcję y = -x w zbiorze liczb rzeczywistych odpowiedz:
– czy jest to funkcja: rosnąca, malejąca, czy stała?
– przez które ćwiartki układu współrzędnych przechodzi ta funkcja?
Mając funkcję y = 6 w zbiorze liczb rzeczywistych odpowiedz:
– czy jest to funkcja: rosnąca, malejąca, czy stała?
– przez które ćwiartki układu współrzędnych przechodzi ta funkcja?
Mając funkcję \(y=-\frac{1}{2}x-2\) w zbiorze liczb rzeczywistych odpowiedz:
– czy jest to funkcja: rosnąca, malejąca, czy stała?
– przez które ćwiartki układu współrzędnych przechodzi ta funkcja?
Wykaż, że funkcja f(x) = 5x + 8 jest rosnąca.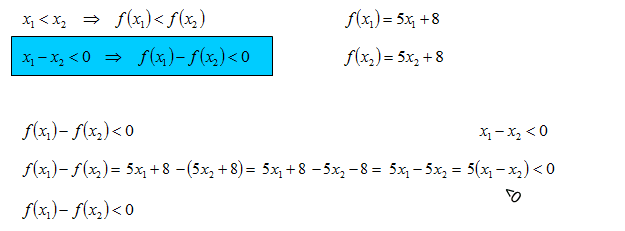
W zadaniu korzystamy z definicji monotoniczności funkcji.
Wykaż z definicji, że funkcja f(x) = -2x + 4 jest malejąca.
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Sprawdź z definicji monotoniczności, czy funkcja f(x) = 4x – 0,5 jest rosnąca, malejąca lub stała.
Treść dostępna po opłaceniu abonamentu.Sprawdź z definicji monotoniczności, czy funkcja f(x) = -5x – 1 jest rosnąca, malejąca lub stała.
Treść dostępna po opłaceniu abonamentu.Monotoniczność funkcji liniowej z parametrem
Podaj dla jakiego parametru p funkcja: y = px + 5 jest rosnąca, malejąca i stała?
Treść dostępna po opłaceniu abonamentu.Podaj dla jakiego parametru p funkcja: y = (p-5)x – 4p jest rosnąca, malejąca i stała?
Treść dostępna po opłaceniu abonamentu.- Co to jest funkcja liniowa
- Wykres funkcji liniowej
- Dziedzina i zbiór wartości funkcji liniowej
- Współczynnik kierunkowy i postać kierunkowa funkcji liniowej
- Prosta równoległa i prosta prostopadła
- Równanie prostej przechodzącej przez dwa punkty
- Miejsce zerowe funkcji liniowej
- Monotoniczność funkcji liniowej
- Funkcja liniowa, a układ równań
- Funkcja liniowa – sprawdzian




