Sprawdzian z funkcji liniowej

Zadanie.

Mając funkcję y = 2x – 3
a) wykonaj wykres funkcji liniowej w zbiorze liczb rzeczywistych
b) odczytaj z wykresu miejsce zerowe funkcji
c) sprawdź na podstawie obliczeń, czy dobrze podałeś współrzędne miejsca zerowego funkcji
d) podaj współrzędne punktów przecięcia wykresu z osiami X i Y
e) dla jakich argumentów wartości funkcji są dodatnie, a dla jakich ujemne (z wykresu i obliczeń)
f) czy punkt (100, 198) należy do wykresu
g) dla jakiego argumentu x wartość funkcji wynosi 4
h) podaj wartość funkcji dla argumentu -10
i) oblicz dla jakich argumentów wartości funkcji są większe od 5

Rozwiązanie:

a) wykonaj wykres funkcji liniowej y = 2x – 3 w zbiorze liczb rzeczywistych,

X	0	2
Y	-3	1

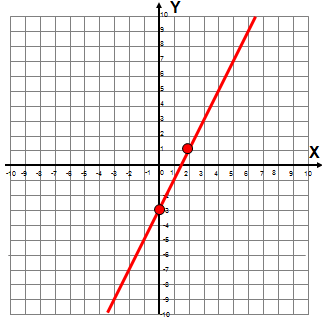b) odczytaj z wykresu miejsce zerowe funkcji y = 2x – 3
\[x = 1\frac{1}{2}\] \[\left( 1\frac{1}{2},0 \right)\] c) sprawdź na podstawie obliczeń, czy dobrze podałeś współrzędne miejsca zerowego funkcji – wykorzystamy tu warunek Y = 0;
\[y = 2x – 3\] \[0 = 2x – 3\] \[-2x = -3\quad \left| \ :\left( -2 \right) \right.\] \[x = \frac{3}{2}\] \[\left( 1\frac{1}{2},0 \right)\] d) podaj współrzędne punktów przecięcia wykresu z osiami X i Y
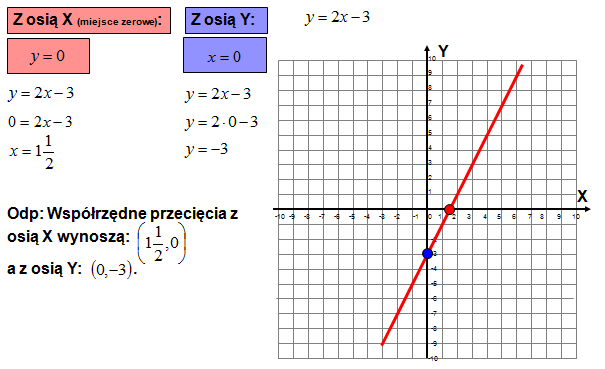e) dla jakich argumentów wartości funkcji są dodatnie, a dla jakich ujemne (z wykresu i obliczeń)
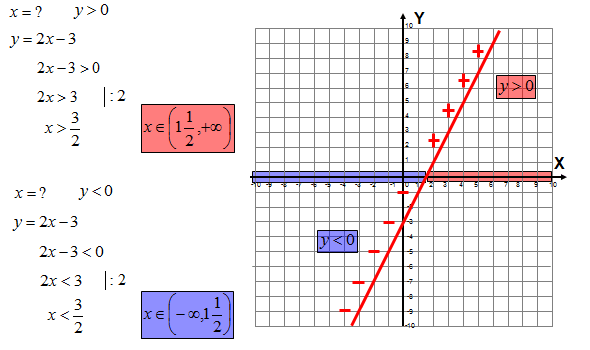f) czy punkt (100, 198) należy do wykresu
\[\begin{align} & \quad \ \ \left( x\ ,\ y \right) \\ & P\left( 100, 198 \right) \\ & y = 2x – 3 \\ & 198 = 2\cdot 100 – 3 \\ & 198\ne 197 \\ \end{align}\] Odp.: Punkt nie (100, 198) nie należy do wykresu funkcji. g) dla jakiego argumentu x wartość funkcji wynosi 4?
\[\begin{align} & \text{x}=\text{?}\quad \text{y}=\text{4} \\ & y = 2x – 3 \\ & 4 = 2x – 3 \\ & -2x = -3 -4 \\ & -2x = -7 \\ & \text{x}=\frac{7}{2}=3\frac{1}{2} \\ \end{align}\] h) podaj wartość funkcji dla argumentu -10
\[\begin{align} & x = -10\quad \text{y}=\text{?} \\ & y = 2x – 3 \\ & y = 2\cdot \left( -10 \right)-3 \\ & \text{y}=-20-\text{3} \\ & \text{y}=-2\text{3} \\ \end{align}\] i) oblicz dla jakich argumentów wartości funkcji są większe od 5. \[\begin{align} & y > 5 \\ & y = 2x – 3 \\ & 2x – 3 > 5 \\ & 2x > 5 + 3 \\ & 2x > 8\quad \left| \ :2 \right. \\ & x > 4 \\ \end{align}\]

Zadanie.

Mając funkcję y = 5x + 7 w przedziale \(\left\langle -3,\left. +\infty \right) \right.\)
a) wykonaj wykres funkcji w przedziale określoności
b) odczytaj i oblicz miejsce zerowe (czy dobrze odczytałeś miejsce zerowe z wykresu funkcji?)
c) podaj dziedzinę i zbiór wartości funkcji
d) podaj współrzędne punktów przecięcia wykresu z osiami X i Y
e) odczytaj z wykresu dla jakich argumentów wartości funkcji są dodatnie, a dla jakich ujemne (odczytany wynik z wykresu poprzyj następnie obliczeniami)
f) czy punkt (-4, 13) należy do wykresu funkcji
g) dla jakiego argumentu x wartość funkcji wynosi 4
h) podaj wartość funkcji dla argumentu -11
i) oblicz dla jakich argumentów wartości funkcji są nie większe od 5
j) oblicz dla jakich argumentów wartości funkcji są nie mniejsze od -1
k) podaj najmniejszą i największą wartość funkcji (o ile istnieje)

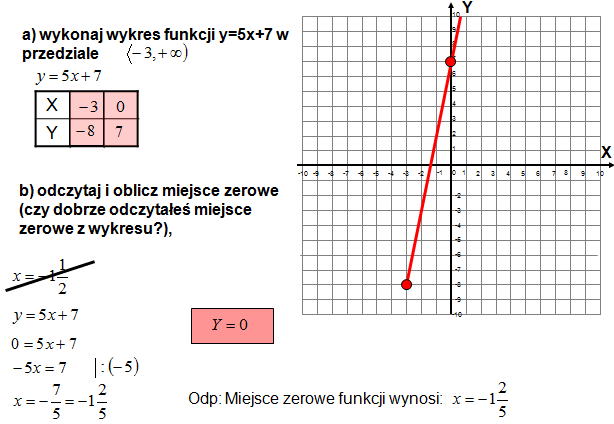Zobacz na YouTube c) podaj dziedzinę i zbiór wartości funkcji
\[\begin{align} & D=\left\langle -3,\left. +\infty \right) \right. \\ & ZW=\left\langle -8,\left. +\infty \right) \right. \\ \end{align}\] d) podaj współrzędne punktów przecięcia wykresu z osiami X i Y,
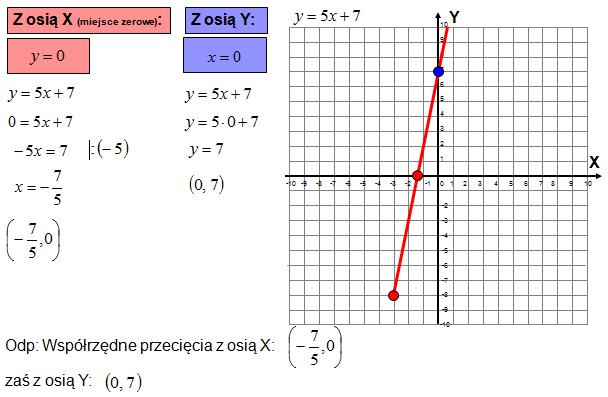e) odczytaj z wykresu dla jakich argumentów wartości funkcji są dodatnie, a dla jakich ujemne (odczytany wynik z wykresu poprzyj następnie obliczeniami)
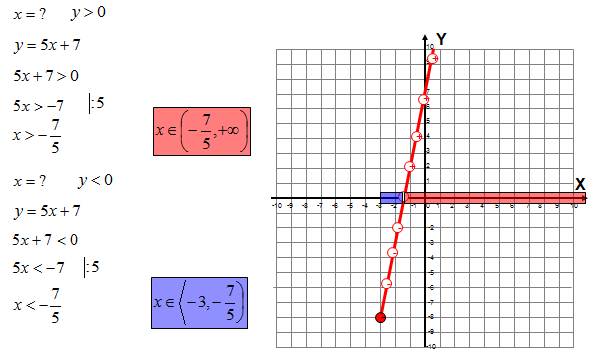f) czy punkt (-4, 13) należy do wykresu funkcji?
\[\begin{align} & \quad \left( x\ ,\ y \right) \\ & P\left( -4, 13 \right) \\ & y = 5x + 7 \\ & 13 = 5\cdot \left( -4 \right)+7 \\ & 13 = -13 \\ \end{align}\] Odp.: Punkt (-4, 13) nie należy do wykresu funkcji.

g) dla jakiego argumentu x wartość funkcji wynosi 4
\[\begin{align} & \text{x}=\text{?}\quad \text{y}=\text{4} \\ & y = 5x + 7 \\ & 4 = 5x + 7 \\ & -5x = 3\quad \left| :\left( -5 \right) \right. \\ & x = -\frac{3}{5} \\ \end{align}\] h) podaj wartość funkcji dla argumentu -11
Odp.: Brak wartość funkcji dla argumentu -11, funkcja nie jest określona dla x = -11, ponieważ \(x\in \left\langle -3,\left. +\infty \right) \right.\)
i) oblicz dla jakich argumentów wartości funkcji są nie większe od 5
\[\begin{align} & y\le 5\quad x=? \\ & y = 5x + 7 \\ & 5x + 7\le 5 \\ & 5x\le 5 – 7 \\ & 5x\le – 2\quad \left| :5 \right. \\ & x\le – \frac{2}{5}\quad ,ale\quad D=\left\langle -3,\left. +\infty \right) \right. \\ & zatem\quad -3\le x\le -\frac{2}{5} \\ \end{align}\] j) oblicz dla jakich argumentów wartości funkcji są nie mniejsze od -1
\[\begin{align} & x=?\quad y\ge -1\quad y=5x+7 \\ & 5x + 7\ge -1 \\ & 5x \ge -1-7 \\ & 5x \ge -8\quad \left| :5 \right. \\ & x \ge -\frac{8}{5} \\ \end{align}\] k) podaj najmniejszą i największą wartość funkcji (o ile istnieje) \[ZW=\left\langle -8,\left. +\infty \right) \right.\] Odp.: Najmniejsza wartość funkcji wynosi -8. Największej wartości nie ma w określonym przedziale, który jest dziedziną funkcji.

Zadanie.

Mając funkcję y = -2x – 1 w przedziale \(\left\langle -5,\left. 4 \right) \right.\)
a) wykonaj wykres funkcji w podanym przedziale
b) podaj dziedzinę i zbiór wartości tak określonej funkcji
c) odczytaj z wykresu, a następnie oblicz miejsce zerowe (czy dobrze odczytałeś miejsce zerowe z wykresu)
d) podaj współrzędne punktów przecięcia z osiami X i Y
e) odczytaj z wykresu dla jakich argumentów wartości są dodatnie, a dla jakich ujemne (odczytany wynik z wykresu poprzyj obliczeniami)
f) czy punkt (-1; 1,5) należy do wykresu funkcji
g) dla jakiego argumentu x wartość funkcji wynosi -2
i) oblicz dla jakich argumentów wartości funkcji są nie mniejsze od 1
j) oblicz dla jakich argumentów wartości funkcji są nie większe od -2

Zobacz na YouTube

Zadanie.

Oblicz pole trójkąta ograniczonego dwiema funkcjami: y = 3x + 4 , y = x – 1 i osią Y.

Zadanie.

Mając poniższy rysunek:
a) Podaj wzory funkcji f(x), g(x), k(x)
b) Oblicz miejsce zerowe funkcji k(x)
c) Oblicz współrzędne punktów przecięcia funkcji g(x) i k(x) oraz g(x) i f(x)
d) Pole trapezu ograniczonego trzema funkcjami i osią X

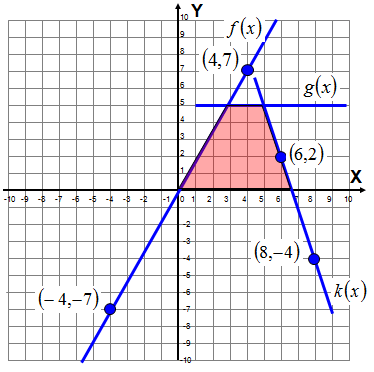Treść dostępna po opłaceniu abonamentu.

Zadanie.

Mając wzory funkcji równoległych f(x) = 5x + b oraz g(x) = ax + 4 wyznacz niewiadome współczynniki a i b postaci kierunkowych funkcji jeśli wiemy, że funkcja f(x) przechodzi przez punkt P(3, 7).

Treść dostępna po opłaceniu abonamentu.

Zadanie.

Oblicz, czy punkt \(P\left( 4;\ 5\frac{2}{7} \right)\) należy do wykresu funkcji \(y=\frac{4}{7}x+3\)? Sprawdź, czy punkt M(-5, 5 ;0) jest miejscem zerowym funkcji.

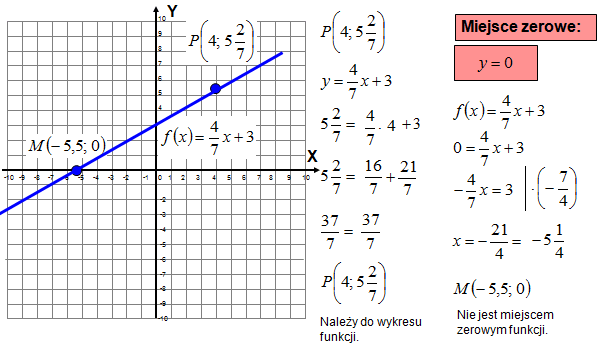Treść dostępna po opłaceniu abonamentu.

Zadanie.

Wyznacz wzory funkcji zawierających się w bokach trójkąta oraz obwód tego trójkąta.

Treść dostępna po opłaceniu abonamentu.

Zadanie.

Dana jest funkcja f(x) = 5x + b₁ przechodząca przez punkt (5, 1) oraz funkcja g(x)=ax + b₂ równoległa do f(x) przechodząca przez punkt (2, 10). Wyznacz literki: a, b₁, b₂.

Treść dostępna po opłaceniu abonamentu.

Zadanie.

Podaj dla jakiego parametru funkcja \(y=\left( p+1 \right)x+{{p}^{2}}+1\) jest rosnąca, malejąca i stała?

Treść dostępna po opłaceniu abonamentu.

Zadanie.

Czy wykresy funkcji opisane wzorami mogą przechodzić przez przyprostokątne w trójkącie prostokątnym?
a) y = 4x – 8 i y = -0,25x + 9
b) y = -3x – 2 i y = ^-1/_{3x + 7}

Treść dostępna po opłaceniu abonamentu.