Postać kierunkowa i współczynnik kierunkowy funkcji liniowej

Podaj wzór funkcji liniowej w postaci równania kierunkowego y = ax + b, jeśli dany jest współczynnik kierunkowy a i współczynnik b.
a) a = 1, b = -5
b) a =-1, b = -2
c) a = 5, b = 3
d) a = 0, b = 4
e) a = 5, b = 0

Narysuj wykresy funkcji liniowej i wyciągnij wnioski dotyczące współczynnika kierunkowego.
y = 2x + 8
y = 2x + 3
y = 2x
y = 2x – 3
y = 2x – 7

Rozwiązanie

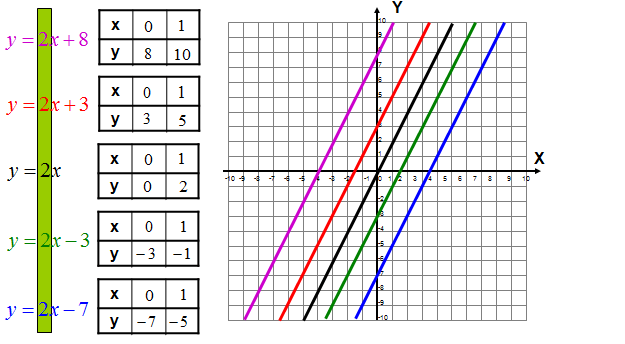
Z pewnością zauważyłeś, że wszystkie wykresy funkcji są równoległe, ponieważ mają taki sam współczynnik kierunkowy.

Podaj przykładowe wzory funkcji liniowych równoległych do funkcji: \(y=-\frac{1}{2}x \)

W zadaniu oczywiście należy budować taki wzór funkcji liniowej, który ma taki sam współczynnik kierunkowy „a”. W tym wypadku \(a=-\frac{1}{2}.\)

Mając wykresy funkcji wyciągnij wnioski dotyczące współczynnika „b” postaci kierunkowej funkcji y = ax + b.

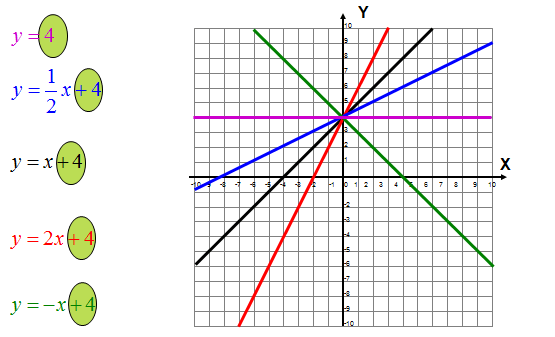
Widzisz, że współczynnik „b” z postaci kierunkowej funkcji liniowej y = ax + b informuje nas o punkcie przecięcia wykresu z osią Y. Inaczej mówiąc punkt przecięcia z osią Y ma współrzędne (0, b).

Mając wykresy funkcji wyciągnij wnioski dotyczące współczynnika b postaci kierunkowej funkcji y = ax + b.

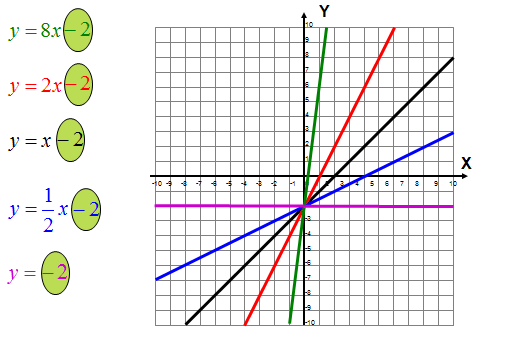
Podobnie jak w zadaniu wyżej widzisz, że wyraz wolny w postaci kierunkowej funkcji liniowej, czyli liczba „-2” określa punkt przecięcia wykresu z osią Y.

Oblicz parametr „a” i „b” wiedząc, że funkcje są równoległe.

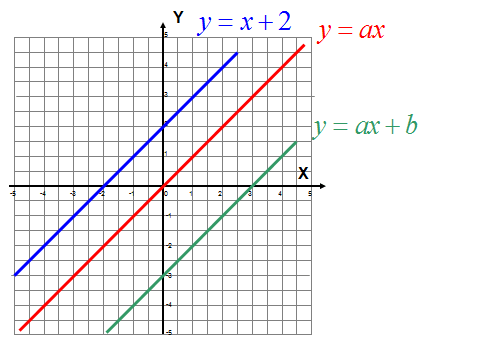
Wszystkie funkcje są równoległe zatem współczynnik kierunkowy a = 1, tak jak w funkcji niebieskiej. Pamiętasz także, że współczynnik „b” wyznacza współrzędną punktu przecięcia wykresu z osią Y. Stąd funkcja czerwona ma współczynnik b = 0, ponieważ przecina się z osią Y w zerze, zaś funkcja zielona przecina się z osią Y w -3, zatem wzór zielonej funkcji liniowej wynosi y = 1x – 3

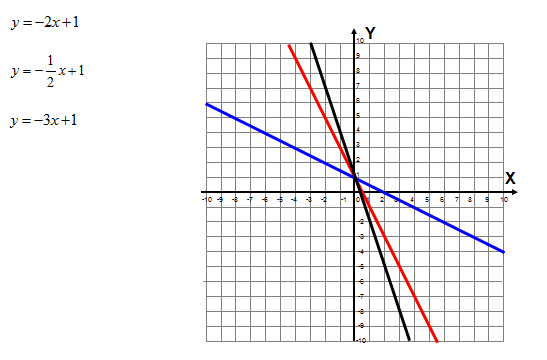
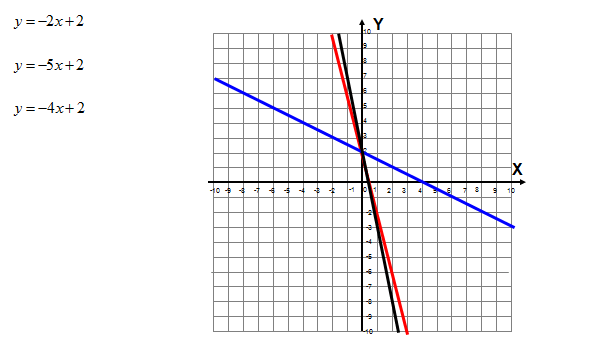
Mając wzory i wykresy funkcji, podaj zależność między współczynnikiem kierunkowym prostej, a kątem nachylenie prostej.

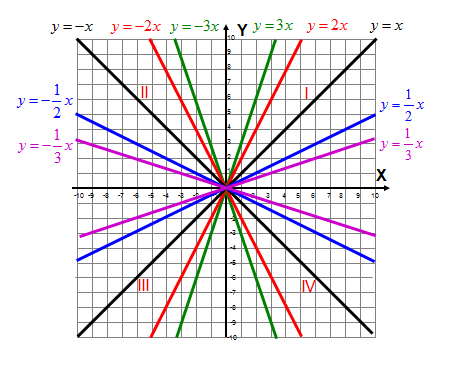
Widzisz, że jeśli współczynnik kierunkowy funkcji liniowej stojący przy x jest dodatni i ma dużą wartość liczbową wówczas wykres staje się bardziej pionowy. Jeśli zaś współczynnik kierunkowy „a” jest ujemny i liczba ujemna jest bardzo mała (z minusem jest duża wartość liczbowa) to funkcja liniowa również staje się bardziej pionowa.

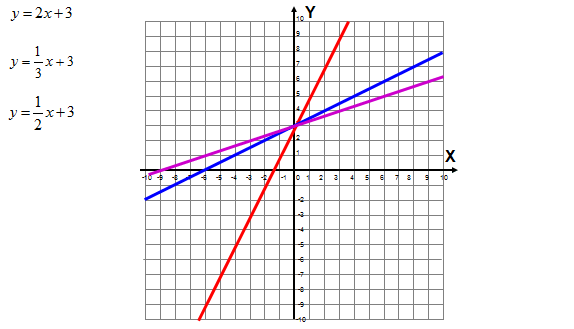
Dopasuj wzory do wykresów funkcji.

Dopasuj wzory do wykresów funkcji.

Dopasuj wzory do wykresów funkcji liniowej.

Podaj wzór funkcji stałej przechodzącej przez punkt P.
a) P(-3, 0)
b) P(-8, 9)
c) P(4, 5)

Narysuj wykres funkcji: \[y=\left\{ \begin{matrix} -x+1\ dla\ x\le 3 \\ 2x-4\ dla\ x> 3 \\ \end{matrix} \right.\]

Narysuj wykres funkcji: \[y=\left\{ \begin{matrix} 2x+12\ dla\ x\le -5 \\ -5\ dla\ -5<x\le 2 \\ -\frac{3}{2}x+10\ dla\ x>2 \\ \end{matrix} \right.\]