Równanie prostej przechodzącej przez dwa punkty
Równanie prostej przechodzącej przez dwa punkty jest przedstawiane zazwyczaj w dwóch równoważnych postaciach. Wzory są w żółtych ramkach.
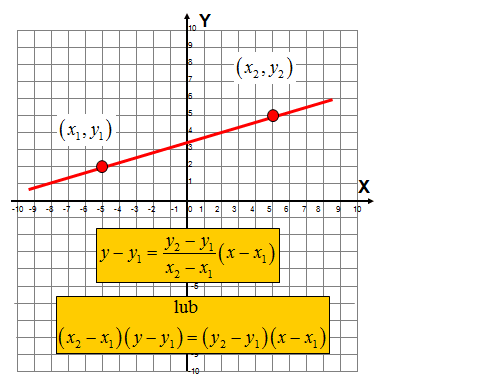
Jest kilka metod dzięki którym możesz podać równanie prostej przechodzącej przez dwa punkty:
- Wzory na równanie prostej przechodzącej przez dwa punkty
- Równanie prostej przechodzącej przez dwa punkty i współczynnik kierunkowy
- Metoda układu równań
Wzory na równanie prostej przechodzącej przez dwa punkty
Zobacz wzory:
\[y-{{y}_{1}}=\frac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\left( x-{{x}_{1}} \right)\] lub \[\left( {{x}_{2}}-{{x}_{1}} \right)\left( y-{{y}_{1}} \right)=\left( {{y}_{2}}-{{y}_{1}} \right)\left( x-{{x}_{1}} \right)\] Są to dwie najczęściej wykorzystywane postacie równania prostej przechodzącej przez dwa punkty.
Podaj wzór funkcji liniowej przechodzącej przez dwa punkty (wykorzystaj wzór).
(2, -3) i (-5, 4)
Rozwiązanie.
Do wzoru: \[\left( {{x}_{2}}-{{x}_{1}} \right)\left( y-{{y}_{1}} \right)=\left( {{y}_{2}}-{{y}_{1}} \right)\left( x-{{x}_{1}} \right)\] Wstawiamy współrzędne punktów: \[\begin{align} & \left( {{x}_{1}},{{y}_{1}} \right)\text{ }i\text{ }\left( {{x}_{2}},{{y}_{2}} \right) \\ & \left( 2,-3 \right)\text{ }i\text{ }\left( -5,4 \right) \\ \end{align}\] Otrzymujemy wyrażenie: \[\left( -5-2 \right)\left( y-\left( -3 \right) \right)=\left( 4-\left( -3 \right) \right)\left( x-2 \right)\] Redukujemy wyrazy podobne: \[-7\left( y+3 \right)=7\left( x-2 \right)\quad \left| :\left( -7 \right) \right.\] Rozwiązujemy równanie: \[y+3=-\left( x-2 \right)\] \[y+3=-x+2\] \[y=-x-1\] Ostatni wiersz jest równaniem prostej przechodzącej przez dwa punkty.Metoda ze współczynnikiem kierunkowym
Podaj wzór funkcji liniowej przechodzącej przez dwa punkty (współczynnik kierunkowy prostej oblicz ze wzoru).
a) (3, 4) i (5, 8)
Rozwiązanie.

Podaj wzór funkcji przechodzącej przez dwa punkty. Współczynnik kierunkowy prostej oblicz ze wzoru. Przez jakie ćwiartki przechodzi wykres funkcji? Określ monotoniczność funkcji.
b) (-2, -3) i (4, -1)
Rozwiązanie.
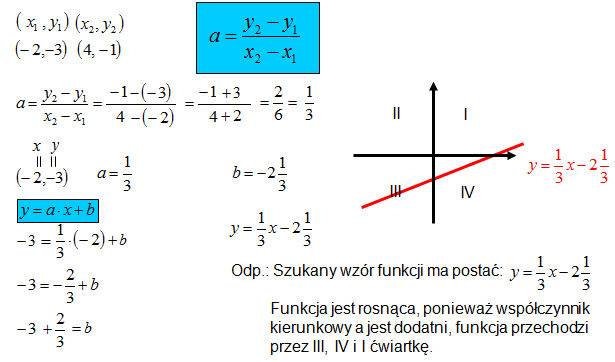
Podaj wzór funkcji przechodzącej przez dwa punkty. Współczynnik kierunkowy prostej oblicz ze wzoru. Określ monotoniczność funkcji.
c) (-1, 2) i (4, 4)
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Metoda układu równań
Przed wykorzystaniem tej metody warto przypomnieć sobie jak rozwiązujemy układy równań?
Podaj wzór funkcji przechodzącej przez dwa punkty: (-3, 0), (4, 5) i nie wykonując wykresu funkcji odpowiedz, czy jest to funkcja rosnąca, malejąca, czy stała?
(Metoda wykorzystująca układy równań).
Podaj wzór funkcji przechodzącej przez dwa punkty: (-3, 6), (-1, 3) i nie wykonując wykresu funkcji odpowiedz, czy jest to funkcja rosnąca, malejąca, czy stała?
Treść dostępna po opłaceniu abonamentu.- Co to jest funkcja liniowa
- Wykres funkcji liniowej
- Dziedzina i zbiór wartości funkcji liniowej
- Współczynnik kierunkowy i postać kierunkowa funkcji liniowej
- Prosta równoległa i prosta prostopadła
- Równanie prostej przechodzącej przez dwa punkty
- Miejsce zerowe funkcji liniowej
- Monotoniczność funkcji liniowej
- Funkcja liniowa, a układ równań
- Funkcja liniowa – sprawdzian




