Nierówności kwadratowe
Nierówności kwadratowe to ważny element działu – funkcja kwadratowa. Musisz wiedzieć już teraz, że rozwiązywanie nierówności kwadratowych wiąże się bezpośrednio z obliczeniem delty i miejsc zerowych(pierwiastków). Do dzieła!
Rozwiązywanie nierówności kwadratowych – zadania
Przekonaj się, jak prosto rozwiązywać nierówności kwadratowe? Zobacz przykładowe zadania do sprawdzianu związane z nierównością kwadratową w filmach. Etapy omawianego zadania zostaną podzielone na poszczególne kroki, które będą wskazówką(szablonem) do rozwiązywania zadań dotyczących nierówności kwadratowych.
Rozwiąż nierówność kwadratową: \(-6{{x}^{2}}+x-1<0\)
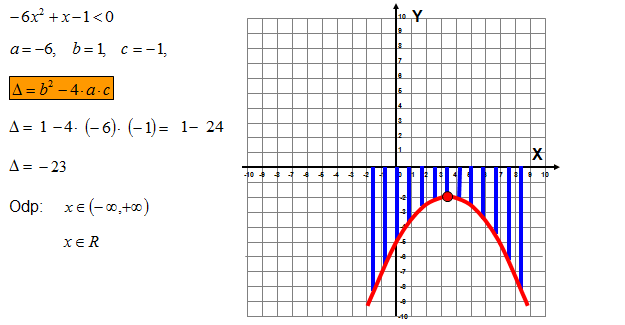
Rozwiązanie nierówności kwadratowych sprowadza się w zasadzie do naszkicowania paraboli. Wystarczą same miejsca zerowe, a następnie określasz czy parabola jest skierowana ramionami do góry (a > 0) czy do dołu (a < 0) – o tym decyduje współczynnik przy x2. Patrząc na znak nierówności określasz, w których przedziałach wykres funkcji jest nad osią X (wartości funkcji są dodatnie), a w których pod osią X (wartości funkcji są ujemne).
W przykładzie wyżej mamy dość osobliwy przypadek, kiedy nie ma miejsc zerowych, ponieważ delta jest mniejsza od zera. Współczynnik przy x2 jest ujemny więc parabola jest skierowana ramionami do dołu. Rysujemy więc przybliżony (a nie dokładny) wykres funkcji kwadratowej. Patrzymy teraz na znak nierówności „<” ,który informuje nas, że rozwiązaniami są ujemne wartości funkcji – te pod osią X. W tym wypadku cały wykres jest pod osią X. Dlatego rozwiązaniami są wszystkie liczby rzeczywiste.
Rozwiąż nierówność kwadratową: \({{x}^{2}}+9x+18>0\)
Krok 1. Wyznaczenie pierwiastków trójmianu kwadratowego. Nierówności kwadratowe rozwiązujesz obliczając na początku pierwiastki trójmianu kwadratowego. Można to zrobić na kilka sposobów:
- korzystając ze znanych wzorów wyznaczasz deltę, następnie pierwiastki trójmianu kwadratowego
- możesz przy pomocy wzorów skróconego mnożenia doprowadzić trójmian kwadratowy do postaci iloczynowej, a patrząc na postać iloczynową już łatwo określić pierwiastki nierówności
- możesz w nierównościach niezupełnych wyłączyć x przed nawias otrzymując w prosty sposób postać iloczynową, a tym samym pierwiastki trójmianu kwadratowego
Wzór na deltę i miejsca zerowe(pierwiastki)
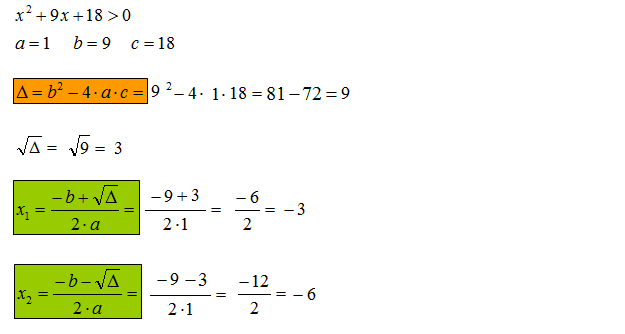
Krok 2. Zaznaczenie pierwiastków w układzie współrzędnych. Mając wyznaczone pierwiastki trójmianu kwadratowego zaznaczasz je w układzie współrzędnych.
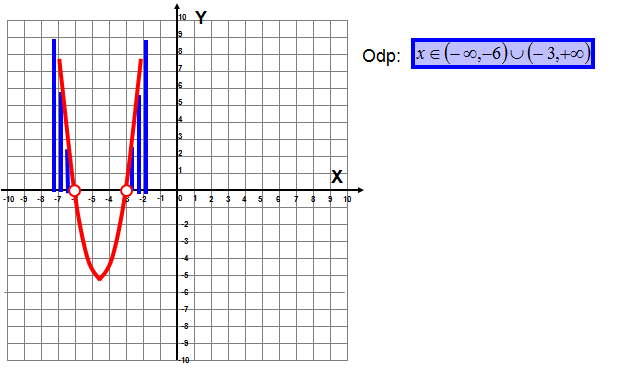
Krok 3. Rysujesz parabolę ramionami skierowanymi do dołu lub do góry.
Jeśli współczynnik „a” trójmianu kwadratowego x2 + bx + c = 0 jest:
- a > 0 to ramiona paraboli są skierowane do góry
- a < 0 to ramiona paraboli są skierowane do dołu
Krok 4. Patrząc na znak nierówności zaznaczasz na rysunku przedział rozwiązań nierówności.
Jeśli wzór wyrażający trójmian kwadratowy: x2 + bx + c jest większy od 0 wówczas zaznaczasz tę część osi X, w której wykres jest powyżej osi X.
Jeśli trójmian kwadratowy: x2 + bx + c jest mniejszy od 0 to zakreskowujemy tą część osi, której wartości są ujemne, czyli wykres leży pod osią X.
Pamiętamy również o zaznaczeniu miejsc zerowych:
- kółkami zamalowanymi jeśli występuje znak nierówności ≥ lub ≤
- kółkami pustymi jeśli masz znaki < lub >
Warto wspomnieć, że znaki ≥ lub ≤ powodują domknięcie przedziałów rozwiązania danej nierówności, zaś znaki < lub > powodują otwarcie tychże przedziałów w wybranych punktach.
Rozwiąż nierówność kwadratową: \(3{{x}^{2}}-75<0\)
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Rozwiąż nierówność kwadratową: \({{x}^{2}}-5x\ge 0\)
Treść dostępna po opłaceniu abonamentu.Rozwiąż nierówność kwadratową: \(-{{x}^{2}}+4x<-5\)
Treść dostępna po opłaceniu abonamentu.Rozwiąż nierówność kwadratową: \(-6{{x}^{2}}+x-1<0\)
Treść dostępna po opłaceniu abonamentu.- Definicja funkcji kwadratowej
- Funkcja kwadratowa – wzory
- Wykres funkcji kwadratowej
- Dziedzina i zbiór wartości funkcji kwadratowej
- Monotoniczność funkcji kwadratowej
- Miejsca zerowe funkcji kwadratowej
- Postać iloczynowa trójmianu kwadratowego
- Równanie kwadratowe
- Równania kwadratowe niezupełne
- Równania sprowadzalne do równań kwadratowych
- Nierówności kwadratowe
- Funkcja kwadratowa – sprawdzian




