Potęga o wykładniku całkowitym ujemnym
Najważniejsze:
- Jeśli chcesz pozbyć się ujemnego wykładnika, usuwasz minus przy jednoczesnym odwróceniu podstawy potęgi.
- Jeśli odwrócisz podstawę, wówczas jednocześnie zmień znak w wykładniku na przeciwny (z plusa na minus lub odwrotnie)
W matematyce potęga o wykładniku całkowitym ujemnym jest zazwyczaj usuwana!
Ujemny wykładnik usuwasz przez odwrócenie liczby, która jest w podstawie potęgi. Najlepiej to zrozumieć poprzez rozwiązanie kilku przykładów.
Potęga o wykładniku całkowitym ujemnym – zadania i rozwiązania
Wykonaj potęgowanie.
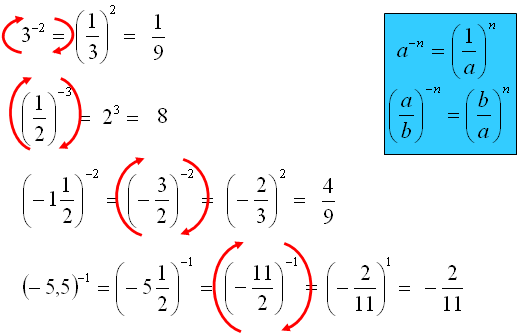
W pierwszym przypadku ujemny wykładnik usuwasz odwracając podstawę 3. A odwrotność liczby 3 to 1/3.
W dwóch ostatnich przykładach musisz najpierw zamienić ułamki na ułamki niewłaściwe (bez całości). Mając licznik i mianownik wówczas usuwasz ujemny wykładnik. Robisz to zamieniając miejscami licznik z mianownikiem przy zachowaniu znaku ułamka. W momencie odwrócenia podstawy usuwasz znak „-” z wykładnika. Zobacz działania na potęgach.
Oblicz x.
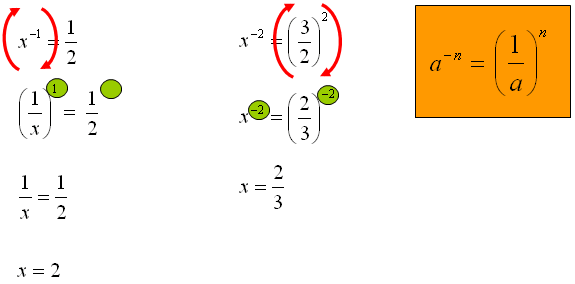
W tego typy prostych równaniach doprowadzasz do równości podstaw lub wykładników. Możesz to zrobić przez usunięcie ujemnego wykładnika bądź też zbudowania ujemnego wykładnika.
Uwaga: W drugim równaniu doprowadzasz do równości wykładników przez stworzenie ujemnego wykładniku. Jeśli masz dodatni wykładnik to podczas odwrócenia podstawy zmienia od znak na przeciwny, czyli ujemny.
Oblicz x.
Zamień potęgi tak, aby były identyczne wykładniki. Możesz to zrobić odwracając jedną z danych podstaw potęg. Masz dwie drogi zamieniasz wykładnik ujemny na dodatni lub też dodatni na ujemny. Za każdym razem podczas zmiany znaku w wykładniku na przeciwny odwracasz podstawę.
Oblicz x.
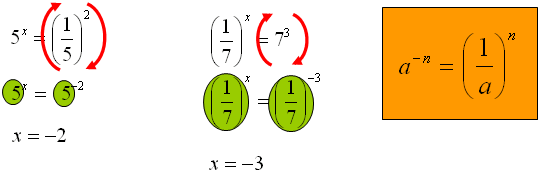
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Oblicz x.
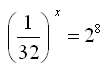Treść dostępna po opłaceniu abonamentu.
W tym przykładzie zauważasz, że można przykład doprowadzić do takiej postaci, w której po obu stronach jest podstawa 2.
Rozpisujesz zatem lewą stronę. Największą trudność może Ci sprawić zauważenie, że 1/32 = (1/2)5. Mając takie same podstawy łatwiej uporać się w całym przykładem.
Widzisz – potęga o wykładniku całkowitym ujemnym to nic trudnego!
- Co to jest potęga
- Potęgi – wzory
- Dodawanie i odejmowanie potęg o tych samych podstawach
- Mnożenie i dzielenie potęg o tych samych podstawach
- Potęga potęgi
- Potęga iloczynu i ilorazu
- Potęga o wykładniku całkowitym ujemnym
- Notacja wykładnicza
- Potęgi – zadania
- Potęgowanie – Sprawdzian
- 8 klasa – Testy online i zadania z potęg i notacji wykładniczej przygotowujące do egzaminu ósmoklasisty