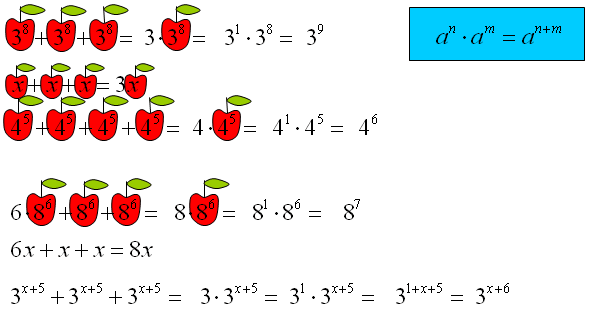Dodawanie i odejmowanie potęg o tych samych podstawach
Nie ma typowych wzorów na dodawanie lub odejmowanie potęg. Zazwyczaj takie działania na potęgach rozwiązuje się, jak w zwykłym dodawaniu typu:
x + x = 2x
y + y = 2y
212 + 212 = 2 · 212 = 213
Można też rozwiązać powyższy przykład wyłączając 212 przed nawias. Spójrz:
212 + 212 = 212 · ( 1 + 1) = 212 · 2 = 213
Są też odrobinę trudniejsze modyfikacje tego zadania na potęgi, ale w takich przypadkach najlepiej wyłącz najniższą potęgę przed nawias.
Dodawanie i odejmowanie potęg – zadania
Liczby a, b i c określone są następująco:
\(a={{3}^{10}}+{{3}^{10}}+{{3}^{10}},\quad b={{3}^{30}}\cdot {{3}^{2}},\quad c={{\left( {{3}^{15}} \right)}^{2}}.\)
Zatem
- a = c PRAWDA/FAŁSZ
- b \(\le \) c PRAWDA/FAŁSZ
- a < b PRAWDA/FAŁSZ
Liczba 21+22+23+…+250 jest podzielna przez
- 2. PRAWDA/FAŁSZ
- 3. PRAWDA/FAŁSZ
- 6. PRAWDA/FAŁSZ
Rozwiązanie:
Na początku warto zauważyć, że jeśli liczba jest podzielna przez 2 i 3 to jest podzielna przez 6 i odwrotnie.
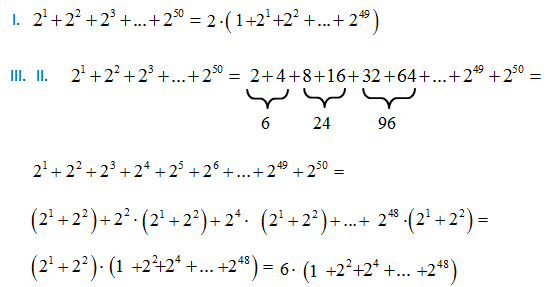
Wykaż, że liczba \({{3}^{22}}+{{6}^{21}}\) jest podzielna przez 5.
Uzasadnij, że dla n naturalnego każda liczba postaci 2n+2n+1+2n+2+2n+3 jest podzielna przez 5.
Ile wynosi wartość wyrażenia 5572 – 4432?
Wykaż, że liczba \({36^{51}} + {9^{50}} – {6^{100}} + {3^{102}}\) jest podzielna przez 5.
Dla dowolnej liczby naturalnej n
- \({{2}^{n-1}}+{{2}^{n-1}}+{{2}^{n-1}}+{{2}^{n-1}}={{2}^{4n-4}}\) PRAWDA/FAŁSZ
- \({{5}^{n-1}}+{{5}^{n-1}}+{{5}^{n-1}}+{{5}^{n-1}}+{{5}^{n-1}}={{5}^{n}}\) PRAWDA/FAŁSZ
- \({{6}^{n-1}}+{{6}^{n-1}}+{{6}^{n-1}}+{{6}^{n-1}}+{{6}^{n-1}}+{{6}^{n-1}}={{6}^{6n}}\) PRAWDA/FAŁSZ
Jeżeli \(a={{6}^{6}}\quad i\quad b={{12}^{3}},\ to\)
- \(a+b=7\cdot {{2}^{8}}\cdot {{3}^{3}}\) PRAWDA/FAŁSZ
- \(a\cdot b={{2}^{12}}\cdot {{3}^{9}}\) PRAWDA/FAŁSZ
- \(\frac{a}{b}={{3}^{3}}\) PRAWDA/FAŁSZ
Ustal, czy liczba \({{123}^{123}}+{{67}^{67}}\) jest podzielna przez 10. Odpowiedź uzasadnij.
Wyrażenie \(2\cdot {{4}^{11}}+3\cdot {{4}^{12}}+8\cdot {{4}^{10}}\) zapisz w postaci jednej potęgi.
Liczba, będąca wartością wyrażenia jest 315+316+317 wielokrotnością liczby:
Dane są liczby: a=610 i b=125. Wtedy
Wykaż, że liczba 20162016+2·20162015+20162014 jest podzielna przez 2017.
Uwaga: Zadanie dotyczy podzielności, ale znakomicie pokazuje na czym polega dodawanie potęg przez wyłączenie wspólnego czynnika przed nawias.- Co to jest potęga
- Potęgi – wzory
- Dodawanie i odejmowanie potęg o tych samych podstawach
- Mnożenie i dzielenie potęg o tych samych podstawach
- Potęga potęgi
- Potęga iloczynu i ilorazu
- Potęga o wykładniku całkowitym ujemnym
- Notacja wykładnicza
- Potęgi – zadania
- Potęgowanie – Sprawdzian
- 8 klasa – Testy online i zadania z potęg i notacji wykładniczej przygotowujące do egzaminu ósmoklasisty