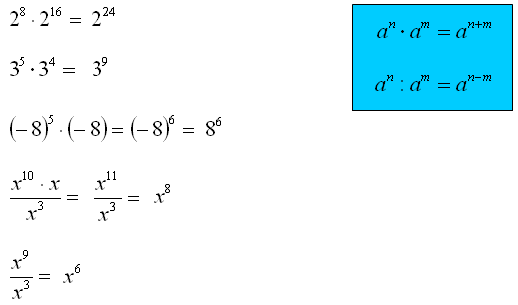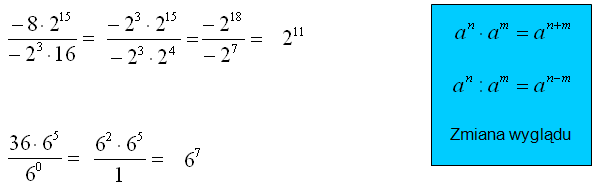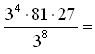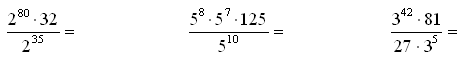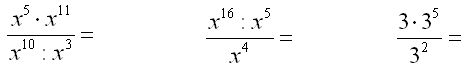Mnożenie i dzielenie potęg o tych samych podstawach
Wykonując mnożenie potęg dodajesz wykładniki, przy dzieleniu potęg odejmujesz wykładniki, a podstawę przepisujesz bez zmiany.
Na pewno zauważysz, że mnożenie i dzielenie potęg o tych samych podstawach rządzi się swoimi prawami, wzorami i własnościami.
Mnożenie i dzielenie potęg – zadania
Poniżej w zadaniach umieszczono w ramkach wykorzystywane wzory na potęgi.
W zadaniu, gdy jest więcej niż dwie potęgi, stosujesz wzory na potęgowanie od lewej do prawej strony. Wykonujesz dodawanie lub odejmowanie wykładników, w zależności od kolejności występującego mnożenia lub dzielenia potęg.
Zadanie. Wykonaj mnożenie i dzielenie potęg o tych samych podstawach.
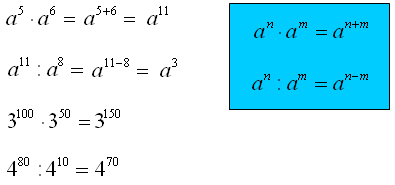
W pierwszym przykładzie tego zadania mając mnożenie potęg o tych samych podstawach dodajemy wykładniki. Widzisz, że a5 · a6 = a · a · a · a · a · a · a · a · a · a · a = a11. Tutaj specjalnie pogrubiłem pierwszą potęgę i jej rozpisaną postać za znakiem „=”. Sądzę, że na tej podstawie widać, że nie ma sensu za każdym razem rozpisywać potęgowania na iloczyn. Zwłaszcza, gdy wykładnik jest dużą liczbą. Po prostu dodajesz wykładniki i zrobione.
W drugim przykładzie wykonując dzielenie potęg o tych samych podstawach odejmujesz od siebie wykładniki.
Wykonaj mnożenie i dzielenie potęg.
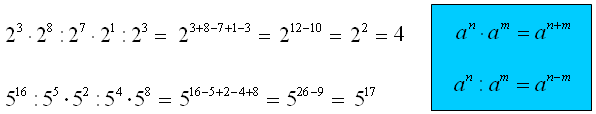
Uwaga: W przypadku, gdy mamy razem wymieszane mnożenie i dzielenie potęg o tych samych podstawach wówczas wykładniki dodajemy lub mnożymy po kolei według zasady „od lewej do prawej”.
W pierwszym przykładzie:
Pierwsze mnożenie potęg powoduje dodawanie wykładników (3 + 8), następnie jest dzielenie potęg więc odejmujemy wykładnik 7 (mamy już 3 + 8 – 7) i tak dalej. Następnie wykonujemy działania dodawania i odejmowania w wykładniku.
Wykonaj mnożenie i dzielenie potęg.
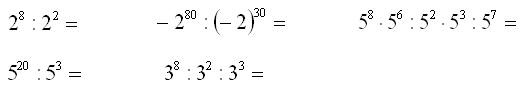
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
W tym zadaniu warto zwrócić uwagę na przykład -280:(-2)30 = . Dzielna: -280 jest liczbą ujemną mimo parzystej potęgi, ponieważ brak nawiasu wokół liczby -2. Dzielnik (-2)30 jest dodatni ponieważ istnieje nawias wokół liczby (-2) i potęga jest parzysta.
Potęgi zmieniające wygląd
Bardzo często omawiając potęgi spotyka się zmianę ich postaci.
Na przykład.
64 = 82 = 43 = 26
W tym przypadku liczba 64 jest potęgą liczby 8, bo 82 = 64, jest też potęgą liczby 4, bo 43 = 64 oraz jest również potęgą liczby 2, ponieważ 26 = 64.
W zadaniach niżej dość często występuje takie zmienianie wyglądu potęgi.
Zapisz poniższe liczby całkowite w postaci potęgi xy
 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Zobacz inne działania na potęgach.
- Co to jest potęga
- Potęgi – wzory
- Dodawanie i odejmowanie potęg o tych samych podstawach
- Mnożenie i dzielenie potęg o tych samych podstawach
- Potęga potęgi
- Potęga iloczynu i ilorazu
- Potęga o wykładniku całkowitym ujemnym
- Notacja wykładnicza
- Potęgi – zadania
- Potęgowanie – Sprawdzian
- 8 klasa – Testy online i zadania z potęg i notacji wykładniczej przygotowujące do egzaminu ósmoklasisty