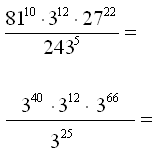Potęga potęgi
Zobacz, jak wygląda wzór: potęga potęgi?
W tym wzorze należy wymnożyć wykładniki potęgi pisane w indeksie górnym, a oddzielone od siebie nawiasem.
Potęga potęgi w zadaniach
Oblicz:

Przykład (23)8, gdybyś chciał rozpisać zgodnie z zasadami potęgowania otrzymałbyś w iloczynie osiem czynników 23 i dalej wykorzystując wzór na mnożenie potęg o tych samych podstawach otrzymałbyś wynik. Taki zapis jednak byłby bardzo uciążliwy. Zatem wystarczy pomnożyć wykładniki potęg i przepisać podstawę bez zmiany.
Oblicz potęgę potęgi.
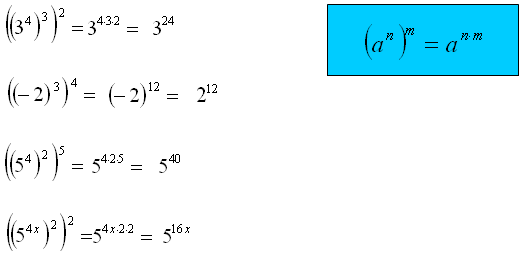
Podane potęgi ustaw w kolejności rosnącej.
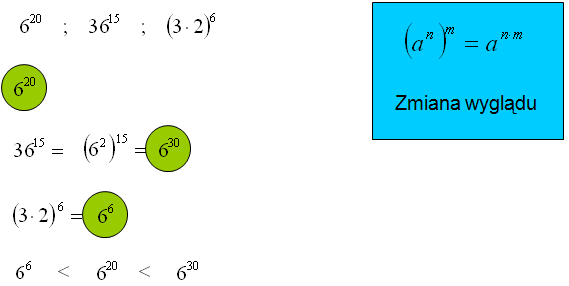
W tym zadaniu sprowadzasz wszystkie potęgi do tej samej podstawy: 6. Pierwszą potęgę przepisujesz bez zmiany, bo już ma podstawę 6. W drugiej liczbie również musisz mieć podstawę 6, zatem „zmieniasz wygląd” liczby 36 na 62. Mając wyrażenie (62)15 stosujesz wzór: „potęga potęgi”, czyli wymnażasz wykładniki: 2 razy 15 i otrzymujesz 630
W ostatniej liczbie dana jest podstawa w postaci iloczynu, więc wymnażasz ją 2 · 3 otrzymując pożądaną podstawę 6.
Uwaga: dla an
Jeśli podstawa a>1 to ta liczba jest większa, która ma większą wartość wykładnika n.
Jeśli podstawa a jest z przedziału (0,1) wówczas ta liczba jest większa, która ma mniejszy wykładnik n.
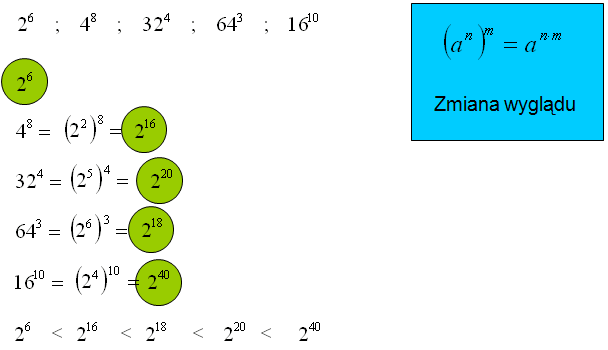
Podane liczby ustaw w kolejności rosnącej.
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
W przykładzie wyżej widzisz, że wszystkie podstawy potęg można sprowadzić do tej samej podstawy: 2. Wystarczy, że zmienisz wygląd podstaw różnych od 2. Na przykład 4 = 22 itd. Oczywiście pamiętasz o przepisaniu wykładnika, który już był na samym początku. Otrzymujesz wówczas wyrażenie: „potęga potęgi” i wymnażając wykładniki otrzymujesz liczby, które łatwo ze sobą porównać.
Uwaga: dla an
Jeśli podstawa a>1 to ta liczba jest większa, która ma większą wartość wykładnika n.
Jeśli podstawa a jest z przedziału (0,1) wówczas ta liczba jest większa, która ma mniejszy wykładnik n.
Podane potęgi ustaw w kolejności rosnącej
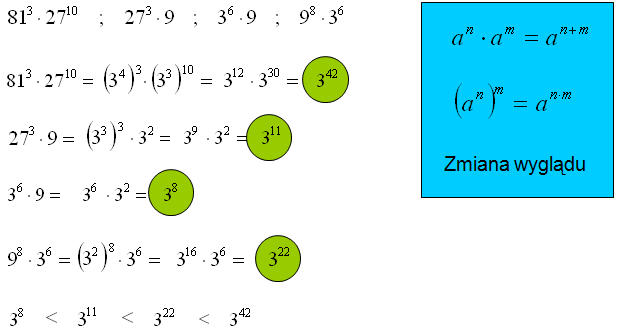 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Uwaga: dla an
Jeśli podstawa a>1 to ta liczba jest większa, która ma większą wartość wykładnika n.
Jeśli podstawa a jest z przedziału (0,1) wówczas ta liczba jest większa, która ma mniejszy wykładnik n.
Podane liczby ustaw w kolejności rosnącej
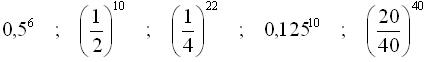 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Uwaga: dla an
Jeśli podstawa a jest z przedziału (0,1) wówczas ta liczba jest większa, która ma mniejszy wykładnik n.
Oblicz połowę liczby: 81000=
Ósmą część liczby: 216=
Trzykrotność liczby 320=
Licząc połowę liczby pamiętaj, że masz dwie możliwości: mnożysz potęgę przez ułamek 1/2 lub dzielisz wyrażenie na 2.
Licząc ósmą część liczby możesz: pomnożyć potęgę przez ułamek 1/8 lub dzielić wyrażenie na 8.
W trzecim przykładzie licząc trzykrotność wymnażasz liczbę przez 3.
Zapisz w jak najprostszej postaci.
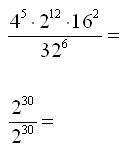 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
W tym zadaniu na początku pamiętaj o sprowadzeniu wszystkich podstaw do jednej podstawy: 2.
W tym dziale zobaczyłeś zadania i rozwiązania związane z pojęciem: „potęga potęgi”. Niekiedy podczas rozwiązywania musieliśmy wspólnie stosować inne wzory na potęgowanie np. na mnożenie i dzielenie potęg o jednakowych podstawach.
Zapraszam do obejrzenia kolejnych zadań zawierających działania na potęgach.
- Co to jest potęga
- Potęgi – wzory
- Dodawanie i odejmowanie potęg o tych samych podstawach
- Mnożenie i dzielenie potęg o tych samych podstawach
- Potęga potęgi
- Potęga iloczynu i ilorazu
- Potęga o wykładniku całkowitym ujemnym
- Notacja wykładnicza
- Potęgi – zadania
- Potęgowanie – Sprawdzian
- 8 klasa – Testy online i zadania z potęg i notacji wykładniczej przygotowujące do egzaminu ósmoklasisty