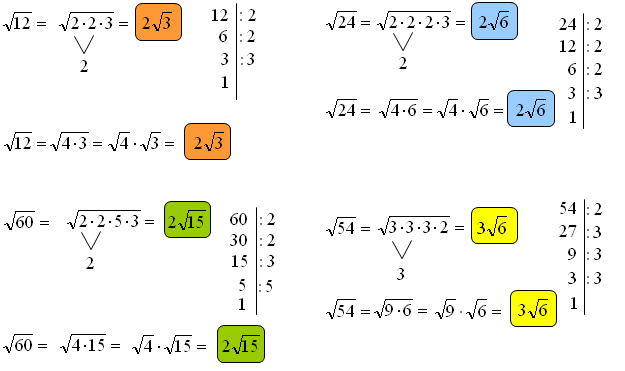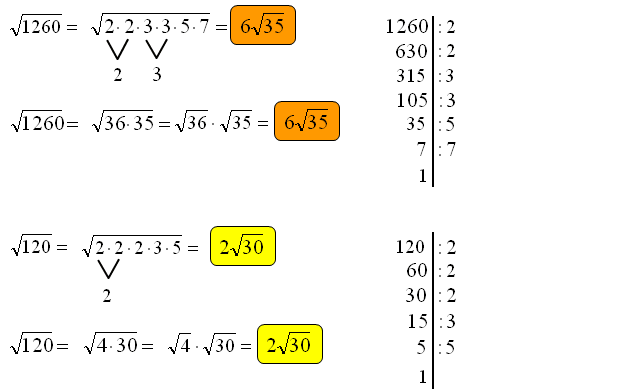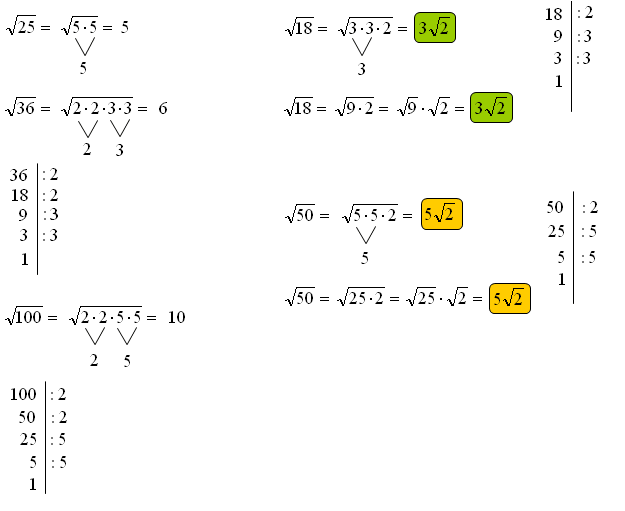Wyłączanie czynnika przed znak pierwiastka
- Definicja pierwiastka
- Pierwiastki – wzory
- Pierwiastek z pierwiastka
- Szacowanie pierwiastków
- Wyłączanie czynnika przed znak pierwiastka
- Włączanie czynnika pod znak pierwiastka
- Mnożenie i dzielenie pierwiastków tego samego stopnia
- Dodawanie i odejmowanie pierwiastków
- Pierwiastek z potęgi
- Usuwanie niewymierności z mianownika
- Potęga o wykładniku wymiernym, a pierwiastkowanie
- 8 klasa – Spis treści powtórek przed egzaminem w tym także pierwiastki
Wyłączanie czynnika przed znak pierwiastka zwłaszcza w początkowej fazie nauki oparte jest głównie na znajomości rozkładu liczby podpierwiastkowej na iloczyn liczb pierwszych.
Liczby pierwsze to liczby posiadające 2 różne dzielniki: „1” i samą siebie. Oto kilka początkowych liczb pierwszych: 2,3,5,7,11,13,17,19,23 itd.
W celu wytłumaczenia rozkładu na czynniki pierwsze posłużę się rozkładem liczby 1260.
Piszesz liczbę 1260, a za nią pionową kreskę (patrz niżej w prawym górnym rogu ilustracji).
Zauważasz, że 2 jest liczbą pierwszą i dzieli liczbę 1260.
Wynik dzielenia 630 wstawiasz pod liczbą 1260.
Dzielisz teraz liczbę 630 na 2, a wynik wpisujesz niżej z lewej strony kreski.
Wykonujesz tak dzielenie biorąc najlepiej kolejne najmniejsze liczby pierwsze.
Dzielenie kończy się liczbą 1 z lewej strony pionowej kreski. Zauważ, że liczba \(1260 = 2\cdot 2\cdot 3\cdot 3\cdot 5\cdot 7\). Jeśli chcesz teraz wyłączyć czynnik przed znak pierwiastka zapisujesz liczbę w postaci iloczynu liczb pierwszych pod znakiem pierwiastka: \[\sqrt{1260}=\sqrt{2\cdot 2\cdot 3\cdot 3\cdot 5\cdot 7}\]
Zauważ, że z iloczynu \(\sqrt{2\cdot 2}\) otrzymujesz „2” przed znakiem pierwiastka. Z iloczynu \(\sqrt{3\cdot 3}\) dostaniesz liczbę „3” wyłączoną przed znak pierwiastka. Wszystkie liczby wyłączone wymnażają się. Zatem \(2\cdot 3=6\). Liczba „6” jest wyłączonym czynnikiem pod znakiem pierwiastka.
Zauważ, że pod pierwiastkiem jest jeszcze liczba „5” i „7”. Jako liczby bez pary nie pierwiastkują się, czyli zostają pod znakiem pierwiastka. Liczby te można wymnożyć.
Podsumujmy: \[\sqrt{1260}=\sqrt{2\cdot 2\cdot 3\cdot 3\cdot 5\cdot 7}=2\cdot 3\sqrt{5\cdot 7}=6\sqrt{35}\]
Wyłączanie czynnika przed znak pierwiastka – przykład
Wyłączanie czynnika przed znak pierwiastka omówię na przykładzie \(\sqrt {18} \)
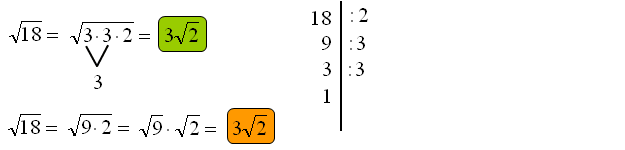
I sposób wyłączania czynnika przed znak pierwiastka
\[\sqrt{18}=\sqrt{3\cdot 3\cdot 2}=3\sqrt{2}\] Rozkładasz liczbę podpierwiastkową 18 na iloczyn liczb pierwszych. Liczby pierwsze to takie, które mają dwa dzielniki: 1 i samą siebie. Możesz to zrobić za pomocą tzw. „kreski” (patrz rys. wyżej). Zauważasz, że liczba 18 zostanie zastąpiona pod pierwiastkiem przez iloczyn: \(3\cdot 3\cdot 2\). Z wyrażenia: \(\sqrt{3\cdot 3}\) otrzymujesz liczbę „3” wyłączoną przed znak pierwiastka. Liczba 2 nie pierwiastkuje się więc zostanie pod pierwiastkiem stąd \(3\sqrt{2}\)
II sposób wyłączania czynnika przed znak pierwiastka
\[\sqrt {18} = \sqrt {9 \cdot 2} = 3\sqrt 2 \] Drugi sposób polega na rozłożeniu liczby, w tym wypadku 18 na taki iloczyn, aby jedna z liczb się pierwiastkowała. Tą liczbą w naszym przypadku jest oczywiście „9”. „9” się pierwiastkuje i otrzymujemy z niej wyłączoną liczbę „3”. Liczba „2” nie pierwiastkuje się zatem zostaje pod znakiem pierwiastka stąd \(3\sqrt{2}\).
Wyłączanie czynnika przed znak pierwiastka – zadania
- Definicja pierwiastka
- Pierwiastki – wzory
- Pierwiastek z pierwiastka
- Szacowanie pierwiastków
- Wyłączanie czynnika przed znak pierwiastka
- Włączanie czynnika pod znak pierwiastka
- Mnożenie i dzielenie pierwiastków tego samego stopnia
- Dodawanie i odejmowanie pierwiastków
- Pierwiastek z potęgi
- Usuwanie niewymierności z mianownika
- Potęga o wykładniku wymiernym, a pierwiastkowanie
- 8 klasa – Spis treści powtórek przed egzaminem w tym także pierwiastki