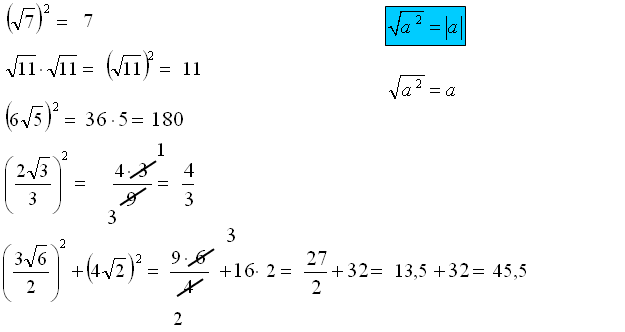Pierwiastek z potęgi

Wykonując działanie: pierwiastek z potęgi pamiętaj, że głównym wzorem jest tutaj: \[\begin{align} & \sqrt[2]{{{x}^{2}}}=\left| x \right| \\ & \sqrt[4]{{{x}^{4}}}=\left| x \right| \\ & \sqrt[6]{{{x}^{6}}}=\left| x \right| \\ & \sqrt[2n]{{{x}^{2n}}}=\left| x \right| \\ & dla\quad \\ & \left| x \right|=\left\{ \begin{matrix} x\quad gdy\quad x\ge 0 \\ -x\quad gdy\quad x<0 \\ \end{matrix} \right. \\ \end{align}\] Zauważ, że w miejsce literki x pod pierwiastkiem możesz wstawić zarówno liczbę dodatnią i ujemną i zawsze wynik będzie dodatni. Potęga parzysta pod pierwiastkiem sprawia, że podstawa pierwiastka będzie zawsze dodatnia.

Wzór \(\sqrt[2]{{{x}^{2}}}=\left| x \right|\) można uprościć do \(\sqrt{{{x}^{2}}}=x\), gdy x≥0.

Z pierwiastkami stopnia nieparzystego potęgi jest znacznie prościej, bo podstawa pierwiastka jak i wynik mogą być liczbami dodatnimi i ujemnymi. \[\begin{align} & {{\sqrt[3]{x}}^{3}}=x \\ & {{\sqrt[5]{x}}^{5}}=x \\ & {{\sqrt[7]{x}}^{7}}=x,\quad itd. \\ \end{align}\]

Kwadrat z pierwiastka

\[\begin{align} & {{\sqrt[2]{x}}^{2}}=x \\ & {{\sqrt[4]{x}}^{4}}=x \\ & {{\sqrt[2n]{x}}^{2n}}=x \\ \end{align}\] Jeśli potęga jest poza znakiem pierwiastka to wynik będzie bez znaku modułu, ponieważ x musi być zawsze dodatni. Wynika to z faktu, że pod znakiem pierwiastka stopnia parzystego podstawa musi być zawsze dodatnia.

Przykłady pierwiastkowania potęgi

\[\begin{align} & \sqrt{{{x}^{4}}}=\sqrt[2]{{{x}^{4}}}\overset{*}{\mathop{=}}\,{{\left| x \right|}^{2}} \\ & \sqrt{{{2}^{4}}}=\sqrt[2]{{{2}^{4}}}\overset{*}{\mathop{=}}\,{{2}^{2}}=4 \\ & \sqrt{{{\left( -2 \right)}^{4}}}=\sqrt[2]{{{\left( -2 \right)}^{4}}}\overset{*}{\mathop{=}}\,{{\left| -2 \right|}^{2}}={{2}^{2}}=4 \\ & \sqrt{{{3}^{8}}}=\sqrt[2]{{{3}^{8}}}\overset{*}{\mathop{=}}\,{{3}^{4}}=81 \\ & \sqrt{{{\left( -3 \right)}^{8}}}=\sqrt[2]{{{\left( -3 \right)}^{8}}}\overset{*}{\mathop{=}}\,{{\left| -3 \right|}^{4}}={{3}^{4}}=81 \\ \end{align}\]

Zauważ, że pierwiastkując pierwiastkiem kwadratowym symbol podniesiony do potęgi parzystej otrzymujesz wynik z modułem. W miejscach oznaczonych gwiazdką (*) oznaczyłem moment, gdy możesz skrócić stopień pierwiastka z potęgą liczby bądź symbolu.

\[\begin{align} & \sqrt[3]{{{x}^{15}}}\overset{*}{\mathop{=}}\,{{x}^{5}} \\ & \sqrt[3]{{{\left( -6 \right)}^{15}}}\overset{*}{\mathop{=}}\,{{\left( -6 \right)}^{5}}=-7776 \\ & \sqrt[5]{{{x}^{20}}}\overset{*}{\mathop{=}}\,{{x}^{4}} \\ & \sqrt[5]{{{7}^{20}}}\overset{*}{\mathop{=}}\,{{7}^{4}} \\ \end{align}\]

Pierwiastki stopnia nieparzystego są w tego typu działaniach odrobinę łatwiejsze. Można skrócić stopień pierwiastka z potęgą, ale nie dopisujemy modułu. Znak jest zachowywany.

Zerknij jak postępujemy w przypadku potęg, które nie skracają się ze stopniem pierwiastka.

\[\begin{align} & \sqrt[3]{{{x}^{8}}}=\sqrt[3]{{{x}^{6}}\cdot {{x}^{2}}}=\sqrt[3]{{{x}^{6}}}\cdot \sqrt[3]{{{x}^{2}}}={{x}^{2}}\sqrt[3]{{{x}^{2}}} \\ & \sqrt{{{6}^{5}}}=\sqrt{{{6}^{4}}\cdot 6}=\sqrt{{{6}^{4}}}\cdot \sqrt{6}={{6}^{2}}\sqrt{6}=36\sqrt{6} \\ & \sqrt[3]{{{4}^{7}}}=\sqrt[3]{{{4}^{6}}\cdot 4}=\sqrt[3]{{{4}^{6}}}\cdot \sqrt[3]{4}={{4}^{2}}\sqrt[3]{4}=16\sqrt[3]{4} \\ & \sqrt[5]{{{9}^{18}}}=\sqrt[5]{{{9}^{15}}\cdot {{9}^{3}}}=\sqrt[5]{{{9}^{15}}}\cdot \sqrt[5]{{{9}^{3}}}={{9}^{3}}\sqrt[5]{{{9}^{3}}}=729\sqrt[5]{{{9}^{3}}} \\ \end{align}\] Liczbę, która jest pod pierwiastkiem należy rozłożyć na taki iloczyn, aby jeden z czynników pierwiastkował się.

Pierwiastek z potęgi – zadania

Zadanie.

Wykonaj działania na pierwiastkach.

x

http://www.youtube.com/watch?v=Nw6OC8jdLxo

Zobacz na stronie

Zobacz na YouTube