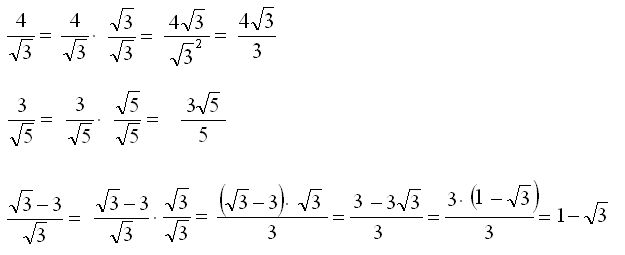Usuwanie niewymierności z mianownika
- Definicja pierwiastka
- Pierwiastki – wzory
- Pierwiastek z pierwiastka
- Szacowanie pierwiastków
- Wyłączanie czynnika przed znak pierwiastka
- Włączanie czynnika pod znak pierwiastka
- Mnożenie i dzielenie pierwiastków tego samego stopnia
- Dodawanie i odejmowanie pierwiastków
- Pierwiastek z potęgi
- Usuwanie niewymierności z mianownika
- Potęga o wykładniku wymiernym, a pierwiastkowanie
- 8 klasa – Spis treści powtórek przed egzaminem w tym także pierwiastki
Rozpatrzmy usuwanie niewymierności z mianownika na podstawie przykładu \(\frac{4}{\sqrt{3}}\). Należy usunąć \(\sqrt{3}\) z mianownika. W tym celu całe wyrażenie należy pomnożyć przez liczbę „1”, a w zasadzie przez ułamek, którego licznikiem i mianownikiem jest \(\sqrt{3}\).
Otrzymujemy w tym momencie zapis \(\frac{4}{\sqrt{3}}\cdot \frac{\sqrt{3}}{\sqrt{3}}\). Dalej mnożysz przez siebie liczniki i mianowniki, otrzymując wynik w usuniętym pierwiastkiem z mianownika: \(\frac{4\sqrt{3}}{3}\)
Jak usunąć niewymierność z mianownika – zadania
Usuń niewymierność (pierwiastek) z mianownika ułamka.
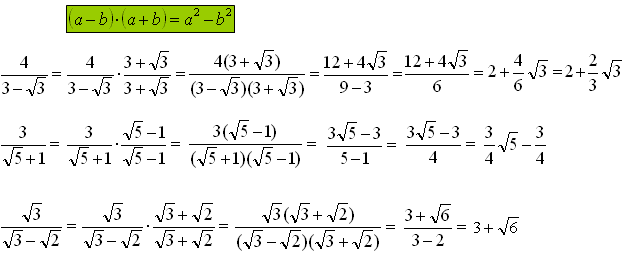
W tego typu zadaniach usuwanie pierwiastka z mianownika polega na utworzeniu i zastosowaniu w mianowniku wzoru skróconego mnożenia podanego w zielonej ramce na ilustracji wyżej.
Zwróć szczególną uwagę na mianownik i licznik dopisywanego ułamka, którego wartość liczbowa jest równa 1 (ponieważ licznik jest równy mianownikowi). Znak między wyrażeniami w dopisywanym ułamku jest zawsze przeciwny do znaku jaki występuje w mianowniku z którego chcemy usunąć pierwiastek. Jeśli w jednym mianowniku jest „+” to w drugim „-” lub odwrotnie.
Wykaż, że liczba \(\frac{1}{7+3\sqrt{3}}+\frac{1}{7-3\sqrt{3}}\) jest wymierna. (Uwaga: usuń niewymierość z mianownika).
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Sprawdź , że \(\sqrt{2}=1+\frac{1}{2+\frac{1}{1+\sqrt{2}}}\)
Treść dostępna po opłaceniu abonamentu.Wyrażenie \({{\left( \frac{4}{\sqrt{3}+1} \right)}^{2}}\) ma wartość:
Usuwanie niewymierności z mianownika ułamka z matury
Liczba \(\frac{{\sqrt {50} – \sqrt {18} }}{{\sqrt 2 }}\) jest równa
Wartość wyrażenia \(\frac{2}{{\sqrt 3 – 1}} – \frac{2}{{\sqrt 3 + 1}} \) jest równa
- Definicja pierwiastka
- Pierwiastki – wzory
- Pierwiastek z pierwiastka
- Szacowanie pierwiastków
- Wyłączanie czynnika przed znak pierwiastka
- Włączanie czynnika pod znak pierwiastka
- Mnożenie i dzielenie pierwiastków tego samego stopnia
- Dodawanie i odejmowanie pierwiastków
- Pierwiastek z potęgi
- Usuwanie niewymierności z mianownika
- Potęga o wykładniku wymiernym, a pierwiastkowanie
- 8 klasa – Spis treści powtórek przed egzaminem w tym także pierwiastki