Prawa De Morgana – Tautologia i inne prawa logiczne
Prawa De Morgana są przykładem praw logicznych – zawsze prawdziwych zdań w logice.
Prawo logiczne inaczej tautologia nazywamy zdanie logiczne, które bez względu na wartości logiczne zdań, z których jest zbudowane zawsze jest prawdziwe. Takie zdanie jest tak „fajnie” zbudowane przy użyciu spójników logicznych, że zawsze będzie prawdziwe.
Jak już wspominałem w tym rozdziale tautologia to zdanie logiczne zawsze prawdziwe niezależnie od doboru wartości logicznych zdań budujących całą tautologię.
Pierwsze prawo De Morgana – zaprzeczenie alternatywy jest koniunkcja zaprzeczeń.
~(p ∨ q) ⇔ ~p ∧ ~q
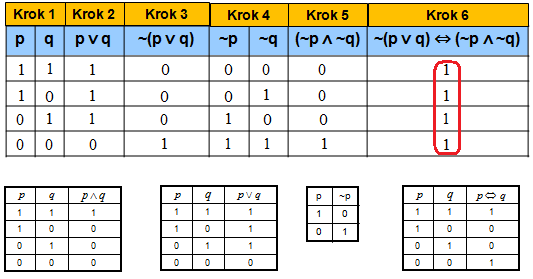
Rozwiązanie:
Drugie prawo De Morgana – zaprzeczenie koniunkcji jest alternatywa zaprzeczeń
~(p ∧ q) ⇔ ~p ∨ ~q
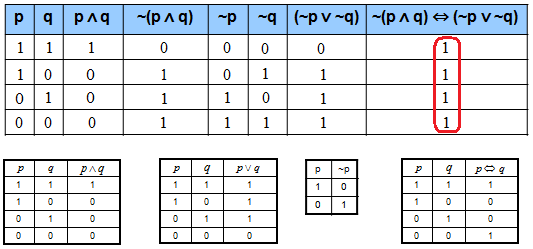
Rozwiązanie:
Prawo podwójnej negacji
~(~p) ⇔ p
Prawo logiczne przemienność alternatywy:
p ∨ q ⇔ q ∨ p
Prawo logiczne przemienność koniunkcji:
p ∧ q ⇔ q ∧ p
Prawo logiczne łączności alternatywy:
(p ∨ q) ∨ r ⇔ p ∨ (q ∨ r)
Prawo łączności koniunkcji:
(p ∧ q) ∧ r ⇔ p ∧ (q ∧ r)
Prawo rozdzielności alternatywy względem koniunkcji:
p ∨ (q ∧ r) ⇔ (p ∨ q) ∧ (p ∨ r)
Prawo rozdzielności koniunkcji względem alternatywy:
p ∧ (q ∨ r) ⇔ (p ∧ q) ∨ (p ∧ r)
Prawo przechodniości implikacji:
[(p ⇒ q) ∧ (q ⇒ r)] ⇒ (p ⇒ r)
Prawo wyłączonego środka:
p ∨ ~p – prawo to mówi, że zawsze prawdziwe jest albo zdanie logiczne, albo jego zaprzeczenie.
Prawo zaprzeczenia implikacji:
~(p ⇒ q) ⇔ p ∧ ~q
Prawo zastąpienia równoważności implikacją:
(p ⇔ q) ⇔ [(p ⇒ q) ∧ (q ⇒ p)]
Prawo kontrapozycji:
(p ⇒ q) ⇔ (~q ⇒ ~p)
Prawo odrywania:
[(p ⇒ q) ∧ p] ⇒ q
Prawo eliminacji implikacji:
(p ⇒ q) ⇔(~p) ∨ q




