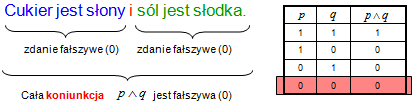Koniunkcja
Koniunkcja dwóch zdań jest prawdziwa, gdy prawdziwe są oba tworzące je zdania.
Koniunkcję można zdefiniować jako dwuargumentowe działanie określone w zbiorze zdań, które zdaniom p, q przyporządkowuje zdanie p i q.
Koniunkcja zadań p, q zapisywana jest przy pomocy spójnika „i” np.: p i q.
W zapisie matematycznym ten spójnik jest również zapisywany przez symbol ∧ np.: p ∧ q.
Tabelka koniunkcji.
| p | q | p ∧ q |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
1 Przykład: Oceń wartość logiczną zdań.
p – „Węgiel jest czarny” (1 – zdanie prawdziwe)
q – „Węgiel jest twardy” (1 – zdanie prawdziwe)
Zdanie do sprawdzenia:
Odpowiedź: Jest to zdanie prawdziwe, ponieważ oba zdania są prawdziwe.
2 Przykład: Oceń wartość logiczną zdań.
p – „Liczba 4 jest parzysta” (1 – zdanie prawdziwe)
q – „Liczba 4 jest podzielna przez 3” (0 – zdanie fałszywe)
Zdanie do sprawdzenia:
Odpowiedź: Pierwsze zdanie logiczne jest prawdziwe, drugie zaś fałszywe, zatem cała koniunkcja na mocy tabelki jest fałszywa.
3 Przykład: Oceń wartość logiczną zdań.
p – „-3 jest liczbą naturalną” (0 – zdanie fałszywe)
q – „-3 jest liczbą całkowitą” (1 – zdanie prawdziwe)
Zdanie do sprawdzenia:
Odpowiedź: Pierwsze zdanie logiczne jest fałszywe, drugie zaś prawdziwe, zatem cała koniunkcja na mocy tabelki jest fałszywa.
4 Przykład: Oceń wartość logiczną zdań.
p – „Cukier jest słony” (0 – zdanie fałszywe)
q – „Sól jest słodka” (0 – zdanie fałszywe)
Zdanie do sprawdzenia:
Odpowiedź: Pierwsze zdanie jest fałszywe, drugie też jest fałszywe, zatem cała koniunkcja na mocy tabelki jest fałszywa.