Metoda zero jedynkowa w logice
Metoda zero jedynkowa jest podstawową metodą dowodzenia zdań logicznych. Najczęściej wykorzystuje się ją do sprawdzania, czy zdanie logiczne jest tautologią?
Tautologia to zdanie zawsze prawdziwe niezależnie od wartości logicznych zadań budujących całą tautologię.
Dokładniejsze omówienie tej metody na podstawie pierwszego prawa De Morgana. Wykażemy, że to zdanie jest zawsze prawdziwe, czyli jest tautologią.
Pierwsze prawo De Morgana – zaprzeczenie alternatywy jest koniunkcją zaprzeczeń.
~(p ∨ q) ⇔ ~p ∧ ~q
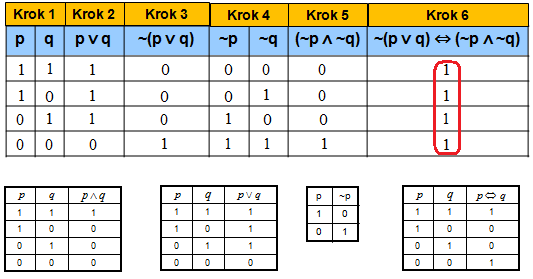
Krok 1: Wypisujemy wszystkie możliwe wzajemne wystąpienia prawdy i fałszu w zdaniach p i q. Przy dwóch zdaniach mamy możliwości (wierszy w tabelce) 22=4. W wyrażeniu składajacym się z np. 3 zdań składowych mamy ich już 23=8.
Krok 2: Badamy wartości logiczne poszczególnych części składowych zdań budujących całe wyrażenie. W naszym przypadku wypisujemy wartości logiczne 1 lub 0 dla alternatywy (p ∨ q).
Krok 3: Zaprzeczamy alternatywę (p ∨ q) z kroku 2. Otrzymana kolumna jest jednocześnie lewą stroną równoważności.
Krok 4: Wypisujemy wartości logiczne negacji zadania p i zdania q.
Krok 5: Mając już ~p i ~q korzystając z tabelki koniunkcji wyznaczamy (~p ∧ ~q). Otrzymana kolumna jest prawą stroną równoważności.
Krok 6: Wyznaczamy wartość całego zdania. Patrzymy, czy równoważność jest prawdziwa. Porównujemy lewą stronę równoważności wyznaczoną w kroku 3 i prawą stronę równoważności wyznaczoną w kroku 5. Jeśli lewa i prawa strona dla każdego wiersza będzie sobie równa to w ostatniej kolumnie zapisujemy jedynkę – 1. Wystąpienie samych jedynek informuje nas, że jest to tautologia, czyli zdanie zawsze prawdziwe.
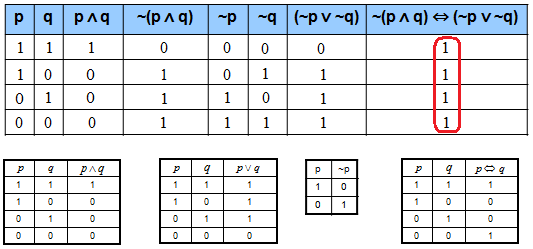
Drugie prawo De Morgana – zaprzeczenie koniunkcji jest alternatywą zaprzeczeń
~(p ∧ q) ⇔ ~p ∨ ~q