Szacowanie pierwiastków kwadratowych, sześciennych i ujemnych
- Definicja pierwiastka
- Pierwiastki – wzory
- Pierwiastek z pierwiastka
- Szacowanie pierwiastków
- Wyłączanie czynnika przed znak pierwiastka
- Włączanie czynnika pod znak pierwiastka
- Mnożenie i dzielenie pierwiastków tego samego stopnia
- Dodawanie i odejmowanie pierwiastków
- Pierwiastek z potęgi
- Usuwanie niewymierności z mianownika
- Potęga o wykładniku wymiernym, a pierwiastkowanie
- 8 klasa – Spis treści powtórek przed egzaminem w tym także pierwiastki
Zanim zaczniesz wykonywać szacowanie pierwiastków sześciennych lub ujemnych, poznaj szacowanie pierwiastków kwadratowych.
Jak można oszacować \(\sqrt{50}\)?
Szukasz dwóch pierwiastków leżących na osi liczbowej najbliżej danego szacowanego pierwiastka. Szukane pierwiastki muszą się pierwiastkować do liczby całkowitej. Jeden z nich musi być większy, a drugi mniejszy od szacowanego pierwiastka.
W naszym przypadku większym pierwiastkiem jest \(\sqrt{64}\), zaś mniejszym \(\sqrt{49}\). Stąd otrzymujemy nierówność: \[\sqrt{49}<\sqrt{50}<\sqrt{64}\]
Jak już wspomniałem pierwiastki ograniczające szacowany pierwiastek muszą się pierwiastkować do liczby całkowitej, zatem mamy: \[\sqrt{49}<\sqrt{50}<\sqrt{64}\] \[7<\sqrt{50}<8\]
W tym momencie oszacowaliśmy \(\sqrt{50}\). Możemy powiedzieć, że leży on na osi liczbowej między liczbą 7, a 8. Choć nie trudno zauważyć, że \(\sqrt{50}\) leży bliżej liczby 7, niż liczby 8. Bo liczba 50 leży bliżej liczby 49 ,niż liczby 64.
Szacowanie pierwiastków kwadratowych – zadania
Wykonaj szacowanie pierwiastków, czyli odpowiedz między jakimi liczbami całkowitymi na osi liczbowej leży dany pierwiastek?
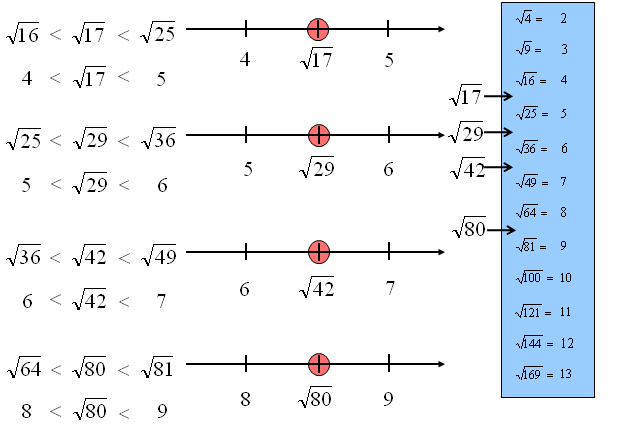
Jak szacować pierwiastki omówię na przykładzie \(\sqrt {17} \). Zauważamy, że \(\sqrt {17} \) leży na osi liczbowej między \(\sqrt {16} \), a \(\sqrt {25} \). Pamiętaj, aby dobierając pierwiastki ograniczające wybierać takie, które po wykonaniu pierwiastkowania dają sąsiednie liczby całkowite. Zatem:
\[\begin{array}{*{20}{c}} {\sqrt {16} }\\ {\begin{array}{*{20}{c}} \Downarrow \\ 4 \end{array}} \end{array}\begin{array}{*{20}{c}} < \\ {\begin{array}{*{20}{c}} {}\\ < \end{array}} \end{array}\begin{array}{*{20}{c}} {\sqrt {17} }\\ {\begin{array}{*{20}{c}} {}\\ {\sqrt {17} } \end{array}} \end{array}\begin{array}{*{20}{c}} < \\ {\begin{array}{*{20}{c}} {}\\ < \end{array}} \end{array}\begin{array}{*{20}{c}} {\sqrt {25} }\\ {\begin{array}{*{20}{c}} \Downarrow \\ 5 \end{array}} \end{array}\]Szacowanie pierwiastków sześciennych – zadania
Wykonaj szacowanie pierwiastka sześciennego, czyli między jakimi liczbami całkowitymi na osi liczbowej leży dany pierwiastek?
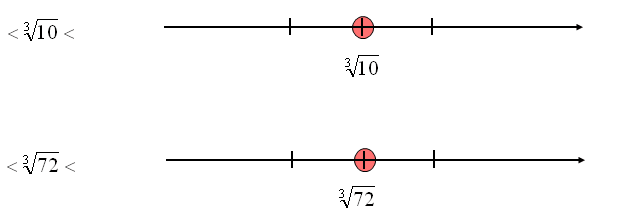
Szacowanie pierwiastków sześciennych robisz podobnie do szacowania pierwiastków kwadratowych. Waźmy na przykład \(\sqrt[3]{{10}}\). Szukamy dwóch pierwiastków sześciennych ograniczających dany pierwiastek z dołu i góry. Ważne jest, aby szukane pierwiastki sześcienne po wykonaniu pierwiastkowania dały nam kolejne liczby całkowite. Pierwiastkiem ograniczającym \(\sqrt[3]{{10}}\) z dołu jest \(\sqrt[3]{{8}}=2\), zaś z góry \(\sqrt[3]{{27}}=3\). Z powyższego szacowania wynika, że \(2<\sqrt[3]{10}<3\).
Możemy powiedzieć, że \(\sqrt[3]{{10}}\) jest równy „dwa z kawałkiem”.
Szacowanie pierwiastków ujemnych – zadania
Między jakimi liczbami całkowitymi na osi liczbowej leży dany pierwiastek?
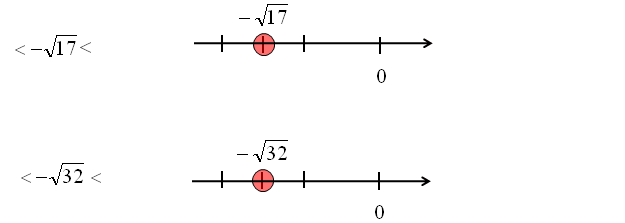
Szacowanie ujemnych pierwiastków jest podobne do szacowania dodatnich pierwiastków. Należy jednak zwrócić szczególną uwagę na liczby w ujemnej części osi liczbowej.
Bardzo częstym błędem jest zamienienie miejscami ujemnych pierwiastków ograniczających szacowany pierwiastek.
Niżej poprawne obliczenie związane z szacowaniem pierwiastków ujemnych.
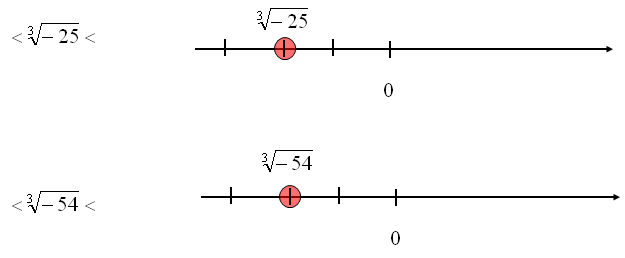
\[\begin{array}{*{20}{c}} { – \sqrt {25} }\\ {\begin{array}{*{20}{c}} \Downarrow \\ { – 5} \end{array}} \end{array}\begin{array}{*{20}{c}} < \\ {\begin{array}{*{20}{c}} {}\\ < \end{array}} \end{array}\begin{array}{*{20}{c}} { – \sqrt {17} }\\ {\begin{array}{*{20}{c}} {}\\ { – \sqrt {17} } \end{array}} \end{array}\begin{array}{*{20}{c}} < \\ {\begin{array}{*{20}{c}} {}\\ < \end{array}} \end{array}\begin{array}{*{20}{c}} { – \sqrt {16} }\\ {\begin{array}{*{20}{c}} \Downarrow \\ { – 4} \end{array}} \end{array}\]Między jakimi liczbami całkowitymi na osi liczbowej leży dany pierwiastek?
- Definicja pierwiastka
- Pierwiastki – wzory
- Pierwiastek z pierwiastka
- Szacowanie pierwiastków
- Wyłączanie czynnika przed znak pierwiastka
- Włączanie czynnika pod znak pierwiastka
- Mnożenie i dzielenie pierwiastków tego samego stopnia
- Dodawanie i odejmowanie pierwiastków
- Pierwiastek z potęgi
- Usuwanie niewymierności z mianownika
- Potęga o wykładniku wymiernym, a pierwiastkowanie
- 8 klasa – Spis treści powtórek przed egzaminem w tym także pierwiastki




